��Ŀ����
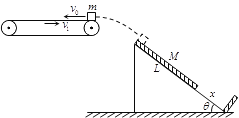
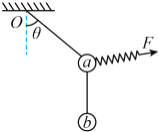
����Ŀ����ͼ��ʾ��A��B��С��ͨ����l=10m�IJ����쳤���������ӣ�A������mA=0.6kg��B������mB=0.4 kg���������ͬһλ���Ⱥ��ͷţ����ͷ�A��t1=1 s�����ͷ� B��ϸ����ֱ���������ϣ��ұ���ʱ�伫�̣����Ϻ�A��B�����پ���t2=2 sͬʱ��ء� ������Ϊ�ʵ㣬���ƿ����������������ٶ�g=10 m/s2��
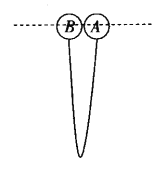
��1���ֱ���ϸ����ֱǰ˲��A��B����ٶȴ�С��
��2���������ͷ�λ�������ĸ߶ȡ�
���𰸡�(1)vA=15m/s,vB=5m/s (2)H=49.25m
��������
��1����������ֱǰB���˶���ʱ��Ϊt����A���˶���ʱ��Ϊt+t1������
l=![]() (t+t1)2-
(t+t1)2-![]() t2
t2
���:t=0.5s
���˶�ѧ��ʽ�ɵã�
vA=g(t+t1)
vB=gt
���:vA=15m/s
vB=5m/s
��2�����ӱ��Ϲ��̣�ʱ�伫�̣�������ɵ�ϵͳ�����غ㣬����
mAvA+mBvB=mAvA��+mBvB��
�־�ʱ��t2����ͬʱ�ŵأ����У�
h1=vA��t2+![]()
��A���ͷŵ����ӱ�����h2=![]()
��H=h1+h2
���:H=49.25m

��ϰ��ϵ�д�
�����Ŀ