题目内容
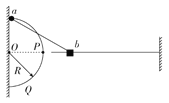
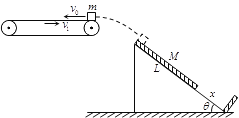
【题目】如图示，质量m=0.5kg的物块（可视为质点）以v0=4m/s的速度从右侧皮带轮最高点向左滑上足够长的水平薄传送带，传送带以v1=2m/s的速度顺时针匀速运动，物块与传送带之间的动摩擦因数μ0=0.2。倾角为θ=37°的固定斜面上静置一质量为M=2kg的薄木板，木板的长度为L=4m，物块与木板之间的动摩擦因数μ1=
，木板与斜面之间的动摩擦因数μ2=
，斜面的底端固定一垂直于斜面的挡板，木板的下端距离挡板为x=2m，木板与挡板碰撞后立即粘在一起停止运动。物块离开传送时做平抛运动，并且恰好沿斜面落在木板的顶端。设物块与木板之间、木板与斜面之间的滑动摩擦力等于最大静摩擦力，则（重力加速度g=10m/s2）：
（1）物块在传送带上运动的过程中，传送带因传送物块多消耗的电能是多少？
（2）皮带轮的最大半径是多少？
（3）物块落在木板以后，通过计算分析物块是否会滑出木板。
【答案】（1）9J；（2）0.4m；（3）没有滑出
【解析】
（1）物块在传送带运动的加速度大小
a0=μ0g=2m/s2，
物块向左减速运动的时间
t1=
=2s，
物块向左减速运动相对皮带的位移
x1=
t1+ v1t1=8m，
物块向右匀加速运动的时间
t2=
=1s，
物块向右匀加速运动相对皮带的位移
x2=v1t2-
t2=1m，
传送带因传送物块多消耗的电能等于传送带克服摩擦力做的功
W=μ0mg（x1+x2）=9J。
（2）物块回到传送带右端的速度为v1=2m/s，要使物块离开传送时做平抛运动，则
解得皮带轮的最大半径
（3）设物块落到斜面上的速度为v3，由平抛的特点知
物块在木板上下滑的加速度
mgsin37°－μ1mgcos37°=ma1
解得a1=-2m/s2，即物块做匀减速运动，而木板的加速度
Mgsin 37°＋μ1mgcos37°－μ2(M＋m)gcos37°=Ma2
解得a2=0.25m/s2，即木板向下做初速度为零的匀加速运动，若木板一直加速运动与挡板碰，设所需时间为t0，则
解得t0=4s；若木板与挡板碰前与木块共速，需时间t3，则
v3＋a1t3=a2t3
解得t3=1.1s；即木板与挡板碰前与木块已经共速，此时共同速度为
v=a2t3=0.28m/s
该过程木板的位移
该过程木块的位移
x1=v3t3+
at32=1.54m
因x1-
x < L，知物块与木板共速前物块没有滑出木板；由于
2=
=
，物块与木板共速后一起沿斜面以0.28m/s的速度匀速运动，木板与挡板碰撞后立即粘在一起停止运动，此后物块沿木板运动的位移
x2=
=
m=0.02m
最终因x1+ x-x < L，物块最终也没有滑出木板。
答：（1）传送带因传送物块多消耗的电能是9J，（2）皮带轮的最大半径为0.4m，（3）没有滑出。
