Question

【题目】在倾角为的固定光滑斜面上有两个用轻弹簧相连的物块A、B，它们的质量分别为m1和m2，弹簧劲度系数为k，C为一固定挡板.系统处于静止状态。现用一平行于斜面向上的拉力拉物块A，使它以加速度a沿斜面向上做匀加速直线运动直到物块B刚要离开挡板C。重力加速度为g，在此过程中

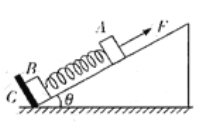
A.拉力的最大值为

B.物块A运动的距离为

C.拉力做功的功率一直增大

D.弹簧弹性势能先减小后增大

Answer 1

【答案】ACD

【解析】

本题考查牛顿第二定律的综合应用。

A. 系统处于静止状态时，弹簧被压缩，设压缩量为x1，由平衡条件得

解得：

x1=

物块B刚要离开挡板C时，弹簧被拉伸，弹簧弹力等于物块B的重力沿斜面方向的分力，设拉伸量为x2.由

解得：

在物块B刚要离开挡板C时，拉力最大，隔离物块A，分析受力，由牛顿第二定律

解得：

故A正确；

B. 物块A在力F作用下沿斜面向上运动直到物块B刚要离开挡板C时，物块A运动的距离为

故B错误；

C. 在拉力拉物块沿斜面向上运动过程中，由于拉力逐渐增大，物块A沿斜面做匀加速运动，速度逐渐增大，根据功率公式P=Fv可知，拉力做功的功率一直增大，故C正确；

D. 由于弹簧原来处于压缩状态，具有弹性势能，在拉力拉物块沿斜面向上运动过程中，弹簧先恢复原长后被拉伸，又具有弹性势能，即弹簧弹性势能先减小后增大，故D正确。

故选ACD。