题目内容
如图所示，质量为mB=14kg的木板B放在水平地面上，质量为mA=10kg的木箱A放在木板B上。一根轻绳一端拴在木箱上，另一端拴在地面的木桩上，绳绷紧时与水平面的夹角为θ=37°。已知木箱A与木板B之间的动摩擦因数μ1=0.5，木板B与地面之间的动摩擦因数μ2=0.4。重力加速度g取10m/s2。现用水平力F将木板B从木箱A下面匀速抽出，试求：（sin37°=0.6，cos37°=0.8）
（1）绳上张力T的大小；
（2）拉力F的大小。
解：（1）对物体A受力分析及建立直角坐标系，如图所示：
∵A静止，受力平衡
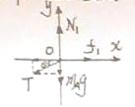∴在x轴上：
Tcosθ=f1 ……①
在y轴上：
N1=Tsinθ+ mAg …②
又∵f1=μ1 N1 ……③
∴由①②③得：
T=100 N
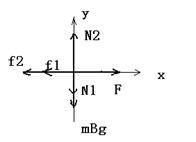(2) 对物体B受力分析及建立直角坐标系，如图所示：
∵B静止，受力平衡
∴在x轴上：
F=f1 + f2 ……④
在y轴上：
N2= N1+mBg ……⑤
又∵f2=μ2 N2 ……⑥
∴由④⑤⑥得：
F =200 N
解析:
略
练习册系列答案
相关题目
（2012?延吉市模拟）如图所示，质量为mB=14kg的木板B放在水平地面上，质量为mA=10kg的木箱A放在木板B上．一根轻绳一端拴在木箱上，另一端拴在地面的木桩上，绳绷紧时与水平面的夹角为θ=37°．已知木箱A与木板B之间的动摩擦因数μ1=0.5，木板B与地面之间的动摩擦因数μ2=0.4．重力加速度g取10m/s2．现用水平力F将木板B从木箱A下面匀速抽出，试求：（sin37°=0.6，cos37°=0.8）
（2008?肇庆二模）如图所示，质量为mB=2kg的平板小车B静止在光滑的水平面上，板的左端静置一质量为mA=2kg的小物体A．一颗质量为10g的子弹以v0=600m/s的水平速度射穿物体A后，子弹速度变为v1=100m/s．物体A与小车B之间的动摩擦因素为μ=0.05，子弹射穿木块的时间很短，g=10m/s2．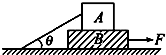
如图所示，质量为mB=14kg的木板B放在水平地面上，质量为mA=10kg的货箱A放在木板B上．一根轻绳一端拴在货箱上，另一端拴在地面，绳绷紧时与水平面的夹角为θ=37°．已知货箱A与木板B之间的动摩擦因数μ1=0.5，木板B与地面之间的动摩擦因数μ2=0.4．重力加速度g取10m/s2．现用水平力F将木板B从货箱A下面匀速抽出，试求：（sin 37°=0.6，cos 37°=0.8）
如图所示，质量为mB=2kg的平板车B上表面水平，开始时静止在光滑水平面上，在平板车左端静止着一块质量为mA=2kg的物体A，一颗质量为m0=0.01kg的子弹以υ0=600m/s的水平初速度瞬间射穿A后，速度变为υ2=100m/s，已知A、B之间的动摩擦因数不为零，且A与B最终达到相对静止． 
如图所示，质量为mB=30kg的长木板B置于光滑水平面上，在长木板B上右侧放一质量mA=20kg的小物体A（可视为质点），现对木板B施加一水平向右的恒力F，且F=120N，使之从静止开始运动．测得木板B在最初t=2.0s内移动的距离为x=5.0m，假设木板B足够长．求：