题目内容
13. 如图所示,一轻弹簧先挂于O点,长度为20cm,当下面挂一10N的重物时,弹簧的长度变为25cm.现用一水平拉力将重物缓慢向右拉动,当弹簧与竖直方向夹角为60°时(弹簧仍在弹性限度内),求:
如图所示,一轻弹簧先挂于O点,长度为20cm,当下面挂一10N的重物时,弹簧的长度变为25cm.现用一水平拉力将重物缓慢向右拉动,当弹簧与竖直方向夹角为60°时(弹簧仍在弹性限度内),求:(1)弹簧的弹力和水平拉力的大小;
(2)重物上升的高度.
分析 (1)分析结点的受力情况,由平衡条件求出弹簧的弹力和水平拉力的大小.
(2)先根据弹簧竖直悬挂时伸长的长度,由胡克定律求出弹簧的劲度系数k,再求出弹簧与竖直方向夹角为60°时伸长的长度,由几何关系求重物上升的高度.
解答  解:(1)以结点为研究对象,其受力情况如图,设弹簧的弹力为T,水平拉力大小为F.
解:(1)以结点为研究对象,其受力情况如图,设弹簧的弹力为T,水平拉力大小为F.
根据平衡条件得:
Tcos60°=mg
Tsin60°=F
解得 T=2mg=20N,F=10$\sqrt{3}$N
(2)弹簧竖直悬挂时,由胡克定律得:G=kx1,得 k=$\frac{G}{{x}_{1}}$=$\frac{10}{0.25-0.20}$=200N/m,此时弹簧的长度为 L1=0.25m
当弹簧与竖直方向夹角为60°时弹簧伸长的长度为 x2=$\frac{T}{k}$=$\frac{20}{200}$m=0.1m
此时弹簧的长度为 L2=x2+L0=0.1m+0.2m=0.3m
重物上升的高度 h=L1-L2cos60°=0.25-0.3×0.5=0.1m
答:
(1)弹簧的弹力和水平拉力的大小分别为20N和10$\sqrt{3}$N;
(2)重物上升的高度是0.1m.
点评 本题是平衡条件与胡克定律的综合应用,分析受力情况是解题的关键,同时要理清几何关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.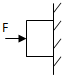 如图所示,用水平力F把铁块压在竖直墙壁上不动,设墙壁对铁块的压力为N,对铁块的摩擦力为f,当F增大时,下面的说法正确的是( )
如图所示,用水平力F把铁块压在竖直墙壁上不动,设墙壁对铁块的压力为N,对铁块的摩擦力为f,当F增大时,下面的说法正确的是( )
 如图所示,用水平力F把铁块压在竖直墙壁上不动,设墙壁对铁块的压力为N,对铁块的摩擦力为f,当F增大时,下面的说法正确的是( )
如图所示,用水平力F把铁块压在竖直墙壁上不动,设墙壁对铁块的压力为N,对铁块的摩擦力为f,当F增大时,下面的说法正确的是( )| A. | N变大,f不变 | B. | N和f均变大 | C. | N和f均不变 | D. | N不变,f变大 |
8.如图所示,带电小球沿直线ab斜向上穿过水平的匀强电场,则下列说法错误的是( )


| A. | 若小球带负电,则电场方向水平向右 | |
| B. | 小球一定做匀减速运动 | |
| C. | 不论小球带何种电荷,电势能总是增加的 | |
| D. | 小球可能沿ab方向做匀速运动 |
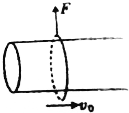 如图所示,足够长的水平直杆上套有一个质量为m的小环,现给小环水平向右的初速度v0,同时对小环施加竖直向上的力F,使F的大小与小环速度v成正比,则小环此后的速度图象不可能是( )
如图所示,足够长的水平直杆上套有一个质量为m的小环,现给小环水平向右的初速度v0,同时对小环施加竖直向上的力F,使F的大小与小环速度v成正比,则小环此后的速度图象不可能是( )



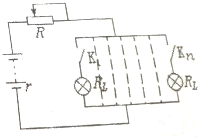 如图所示的电路,电源电动势e=12V,内阻r=1Ω,所接用电器均为“6V,6W”的小灯泡,R是为了保证让电灯正常发光而串联在电路中起分压作用的滑动变阻器,R的最大阻值是4Ω,问:
如图所示的电路,电源电动势e=12V,内阻r=1Ω,所接用电器均为“6V,6W”的小灯泡,R是为了保证让电灯正常发光而串联在电路中起分压作用的滑动变阻器,R的最大阻值是4Ω,问:
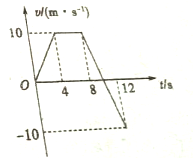 如图所示,是某质点运动的v-t图象,请回答:
如图所示,是某质点运动的v-t图象,请回答: