题目内容
18.倾角为30°的光滑斜面从A点以初速度v0=10m/s将小球往上运动,求经过多长时间小球到达A点下方离A点距离为x=12.5m的B点?分析 物体做匀加速运动,加速度为a,有牛顿运动定律知mgsin30°=ma,根据位移时间关系求解时间.
解答 解:物体做匀变速运动,以向上为正方向,根据牛顿运动定律知mgsin30°=-ma
故a=-gsin30°=-$\frac{1}{2}$g=-5m/s2,v0=10m/s,x=-12.5m
x=${v}_{0}t+\frac{1}{2}a{t}^{2}$
代入数据-12.5=10t$-\frac{1}{2}×10{t}^{2}$
解得t=5s
答:经过5s时间小球到达A点下方离A点距离为x=12.5m的B点.
点评 本题考查牛顿运动定律和匀变速直线运动规律的应用,知道加速度不变的运动为匀变速运动,注意位移方向即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.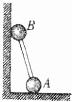 如图,两球通过轻杆连接,A球在水平面上,B球紧靠竖直墙壁,开始时,控制杆与水平方向成53°角,球A的质量为0.1kg,球B的质量为0.2kg,杆长1m,释放后,A球向右滑动,B球沿竖直墙壁下滑,直至杆与水平方向夹角为30°,不计一切摩擦及球的大小,则( )
如图,两球通过轻杆连接,A球在水平面上,B球紧靠竖直墙壁,开始时,控制杆与水平方向成53°角,球A的质量为0.1kg,球B的质量为0.2kg,杆长1m,释放后,A球向右滑动,B球沿竖直墙壁下滑,直至杆与水平方向夹角为30°,不计一切摩擦及球的大小,则( )
 如图,两球通过轻杆连接,A球在水平面上,B球紧靠竖直墙壁,开始时,控制杆与水平方向成53°角,球A的质量为0.1kg,球B的质量为0.2kg,杆长1m,释放后,A球向右滑动,B球沿竖直墙壁下滑,直至杆与水平方向夹角为30°,不计一切摩擦及球的大小,则( )
如图,两球通过轻杆连接,A球在水平面上,B球紧靠竖直墙壁,开始时,控制杆与水平方向成53°角,球A的质量为0.1kg,球B的质量为0.2kg,杆长1m,释放后,A球向右滑动,B球沿竖直墙壁下滑,直至杆与水平方向夹角为30°,不计一切摩擦及球的大小,则( )| A. | 在滑动过程中AB两球速度大小始终相等 | |
| B. | AB两球和杆组成的系统机械能守恒 | |
| C. | 最后A球的速度大小为2m/s | |
| D. | 最后B球的速度大小为$\frac{6\sqrt{7}}{7}$m/s |
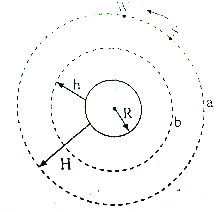 一组太空人乘坐穿梭机,前往修理位于离地球表面H的圆形轨道a上的哈勃望远镜W,机组人员使穿梭机S进入与望远镜相同的轨道并关闭推进火箭,而望远镜则在穿梭机前方数公里处,如图所示.已知地球质量为M,地球半径为R,穿梭机质量为m,则
一组太空人乘坐穿梭机,前往修理位于离地球表面H的圆形轨道a上的哈勃望远镜W,机组人员使穿梭机S进入与望远镜相同的轨道并关闭推进火箭,而望远镜则在穿梭机前方数公里处,如图所示.已知地球质量为M,地球半径为R,穿梭机质量为m,则 如图所示,S1和S2是两列频率相同的相干波源,在某种介质中传播相遇所相成的干涉图样,图中实线表示相干波的波峰,虚线表示相干波的波谷,在干涉波上有A、B、C三个交点,则相干波加强点是B、C、减弱点是A.
如图所示,S1和S2是两列频率相同的相干波源,在某种介质中传播相遇所相成的干涉图样,图中实线表示相干波的波峰,虚线表示相干波的波谷,在干涉波上有A、B、C三个交点,则相干波加强点是B、C、减弱点是A. 如图所示,一轻弹簧先挂于O点,长度为20cm,当下面挂一10N的重物时,弹簧的长度变为25cm.现用一水平拉力将重物缓慢向右拉动,当弹簧与竖直方向夹角为60°时(弹簧仍在弹性限度内),求:
如图所示,一轻弹簧先挂于O点,长度为20cm,当下面挂一10N的重物时,弹簧的长度变为25cm.现用一水平拉力将重物缓慢向右拉动,当弹簧与竖直方向夹角为60°时(弹簧仍在弹性限度内),求: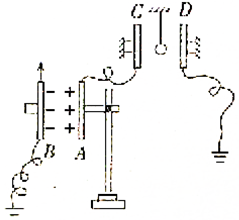 某同学在研究平行板电容器的决定因素实验中,由于手边没有静电计,就再用一个平行板电容器CD作为静电计使用,如图所示,将该平行板电容器沿竖直方向固定在绝缘支架上,并在极板间悬挂一个带正电的小球,现使AB金属板带上等量的异种电荷,B板和D板分别接地,并使A板与C板相连,则:
某同学在研究平行板电容器的决定因素实验中,由于手边没有静电计,就再用一个平行板电容器CD作为静电计使用,如图所示,将该平行板电容器沿竖直方向固定在绝缘支架上,并在极板间悬挂一个带正电的小球,现使AB金属板带上等量的异种电荷,B板和D板分别接地,并使A板与C板相连,则: