题目内容
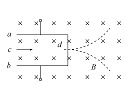
【题目】如图所示，质量M=1kg的木板置于足够长的水平合上，木板的左端与平台左端对齐。在平台的左侧有一水平面，水平面上有一固定的滑块，滑块的上表面有一段光滑水平面和一段光滑圆弧PQ，圆弧和水平面平滑相切于P点，圆弧半径R=1m，所对圆心角为θ=37°，滑块上表面左端有一质量m=2kg的小物块，小物块和滑块左端的固定直挡板间有一根压缩的轻弹簧，小物块和挡板间通过细线连接。Q点与平台间的高度差为h=0.45m。现剪断细线，小物块滑到P点时已经与弹簧脱离，小物块从Q点飞出后恰好沿水平方向从木板左端滑上木板。木板长x=2.5m，小物块与木板间的动摩擦因数μ1=0.2，木板与平台间以及小物块与平台间的动摩擦因数均为μ2=0.1。设小物块滑到平台的瞬间速度没有变化，木板的厚度不计。取g=10m/s2，sin37°=0.6，cos37°=0.8，求：
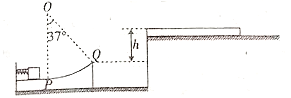
(1)小物块在Q点时对滑块的压力大小；
(2)弹簧的最大弹性势能；
(3)小物块滑离木板后，木板的右端与小物块间的最大距离。
【答案】(1) 
(2) 
(3) 
【解析】
（1）设小物体在Q点时的速度大小为
，滑上木板的左端速度为
，小物块从Q点飞出到水平滑上木板的左端，有：
解得：
小物块在Q点，由牛顿第二定律有：
解得：F=66N
（2）设弹簧的最大弹性势能为
，根据功能关系有：
（3）小物块滑上木板后，物体与木板间的滑动摩擦力
薄木板与平台间的滑动摩擦力
，
小物块向右做匀减速直线运动，木板向右做匀加速直线运动，有：
，
，
小物块从滑上木板到滑离木板时间设为
，由运动学公式有：
解得：
小物块滑离木板时，物块速度设为
，木板速度设为
，有：
小物块滑离木板后两者分别在平台上做匀减速直线运动直到停止，由动能定理有：
解得：
所以，小物块滑离木板后，木块的右端与滑块间的最大距离为：
