题目内容
【题目】已知地球半径R=6390km、自转周期T=24h、表面重力加速度g=9.8m/s2，电磁波在空气中的传播速度c=3×108m/s，不考虑大气层对电磁波的影响。要利用同一轨道上数量最少的卫星，实现将电磁波信号由地球赤道圆直径的一端传播到该直径的另一端的目的，则
A. 卫星数量最少为2颗
B. 信号传播的时间至少为8.52×102s
C. 卫星运行的最大向心加速度为4.9m/s2
D. 卫星绕地球运行的周期至少为24h
【答案】ABC
【解析】试题分析：有几何关系判断需要的卫星的颗数；由几何关系判断出卫星之间的位置，然后由万有引力提供向心力求出卫星的轨道半径，由x=vt求出运动的时间，由万有引力定律求出卫星的向心加速度与周期．
由几何关系可知，过圆的直径的两端的切线是平行的，所以1颗卫星不可能完成将电磁波信号由地球赤道圆直径的一端传播到该直径的另一端的目的，但两颗或两颗以上的卫星接力转播可以实现，所以需要的卫星的最小数目是2颗，A正确；使用2颗卫星传播时，可能有两种情况，如图：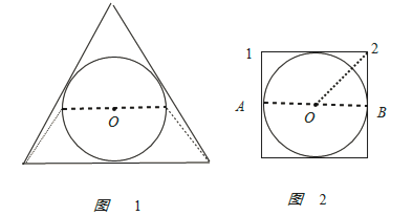
通过图中的比较可知，轨道上有三颗卫星时，将电磁波信号由地球赤道圆直径的一端传播到该直径的另一端的路程更长，则轨道上有三颗卫星时，将电磁波信号由地球赤道圆直径的一端传播到该直径的另一端的时间长．由几何关系可知，在图2中，信号由A→1→2→B的路程的长度为4R，则信号传播的时间： 
，B正确；由图2可知，该卫星对应的半径： 
，卫星的向心加速度
，而地球表面的重力加速度： 
，所以： 
，C正确；同步卫星的周期为24h，而该卫星的半径
，结合： 
可知，该卫星的周期小于24h．故D错误．
练习册系列答案
相关题目
