题目内容
如图所示，质量M=4.0kg的长木板B静止在光滑的水平面上，在其右端放一质量m=1.0kg的小滑块A（可视为质点）。初始时刻，A、B分别以v0=2.0m/s向左、向右运动，最后A恰好没有离开B板。已知A、B之间的动摩擦因素µ=0.40，取g=10m/s2,求：
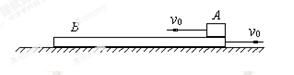
（1）A、B相对运动时的加速度aA和aB的大小和方向；
（2）A相对地面的速度为零时，B相对地面的运动已发生的位移x；
（3）木板B的长度l。
（1）A、B相对运动时的加速度aA和aB的大小和方向；
（2）A相对地面的速度为零时，B相对地面的运动已发生的位移x；
（3）木板B的长度l。
1)aA=4.0m/s2水平向右 aB="1.0" m/s2水平向左 2）x=0.875m 3)l=1.6m
试题分析：（1）A、B分别受到大小为µmg的作用，根据牛顿第二定律
对A物体：µmg=ma
则aA=µg=4.0m/s2 方向水平向右
对B物体：µmg=MaB
aB=µmg/M=1.0m/s2 方向水平向左
（2）开始阶段A相对地面向左匀减速运动，速度为0的过程中所用时间为t1,则v0=aAt1，则t1=v0/aA=0.50s
B相对地面向右做减速运动x = v0t - aBt2/2 =" 0.875m"
⑶ A向左匀减速运动至速度为零后，相对地面向右做匀加速运动，
加速度大小仍为aA = 4.0m/s2
B板向右仍做匀减速运动，
加速度大小仍aB = 1.0m/s2
当A、B速度相等时，A相对B滑到最左端，恰好不滑出木板，
故木板B的长度为这个全过程中A、B间的相对位移；
在A相对地面速度为零时，B的速度vB = v0 – aBt1 = 1.5m/s
设由A速度为零至A、B相等所用时间为t2，则 aAt2 = vB – aBt2，
解得t2 = vB/(aA + aB) = 0.3s
共同速度v = aAt2= 1.2m/s
A向左运动位移xA = (v0－ v)(t1 + t2)/2 =" (2" – 1.2)(0.5 + 0.3)/2 m = 0.32m
B向右运动位移xB = (v0+ v) (t1 + t2)/2 =" (2" + 1.2)(0.5 + 0.3)/2 m =1.28m
B板的长度l = xA + xB = 1.6m
练习册系列答案
相关题目
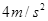，运动过程中的最大速度为
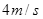，绕标杠时需减速到零，减速的加速度大小为
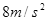，返回时达到最大速度后不再减速，保持最大速度冲到出发点，求该同学往返的总时间t，（绕杆时间忽略不计）
