题目内容
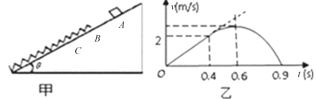
【题目】如图甲所示,在倾斜角为θ的光滑斜面上放一轻质弹簧,其下端固定,静止时上端位置在B点,在A点放上一质量m=2.0 kg的小物体,小物体自由释放,从开始的一段时间内的v–t图象如图乙所示,小物体在0.4 s时运动到B点,在0.9 s到达C点,BC的距离为1.2 m(g=10 m/s2),由图知
A.斜面倾斜角θ=60°
B.物块从B运动到C的过程中机械能守恒
C.在C点时,弹簧的弹性势能为16 J
D.物块从C点回到A点过程中,加速度先增后减,再保持不变
【答案】C
【解析】由图乙所示图象可知,在0~4 s内,物块做匀加速直线运动,加速度为:![]() ,由牛顿第二定律得:mgsin θ=ma,解得:
,由牛顿第二定律得:mgsin θ=ma,解得: ![]() ,则θ=30°,故A错误;从B到C过程,除重力做功外,弹簧弹力对物块最负功,物块的机械能不守恒,故B错误;由能量守恒定律可得,在C点弹簧的弹性势能为:Ep=
,则θ=30°,故A错误;从B到C过程,除重力做功外,弹簧弹力对物块最负功,物块的机械能不守恒,故B错误;由能量守恒定律可得,在C点弹簧的弹性势能为:Ep=![]() mvB2+mghBC=
mvB2+mghBC=![]() ×2×22+2×10×1.2sin30°=16 J,故C正确;物块从C点回到A点过程中,开始弹簧的弹力大于重力沿斜面向下的分力,合力向上,物块向上做加速运动,弹力逐渐减小,物块所受合力减小,物块的加速度减小,然后弹簧的弹力小于重力沿斜面向下的分力,合力向下,物块做减速运动,随物块向上运动,弹簧弹力变小,物块受到的合力变大,加速度变大,当物体与弹簧分离后,物块受到的合力等于重力的分力,加速度不变,物块做加速度不变的减速运动,由此可知在整个过程中,物块的加速度先减小后增大,再保持不变,故D错误;故选C。
×2×22+2×10×1.2sin30°=16 J,故C正确;物块从C点回到A点过程中,开始弹簧的弹力大于重力沿斜面向下的分力,合力向上,物块向上做加速运动,弹力逐渐减小,物块所受合力减小,物块的加速度减小,然后弹簧的弹力小于重力沿斜面向下的分力,合力向下,物块做减速运动,随物块向上运动,弹簧弹力变小,物块受到的合力变大,加速度变大,当物体与弹簧分离后,物块受到的合力等于重力的分力,加速度不变,物块做加速度不变的减速运动,由此可知在整个过程中,物块的加速度先减小后增大,再保持不变,故D错误;故选C。

练习册系列答案
相关题目