题目内容
(7分)已知地球半径为R,地球表面处的重力加速度为g,不考虑地球自转的影响。
(1)推导第一宇宙速度v的表达式;
(2)若已知地球自转的周期为T,求地球同步卫星距离地面的高度h。
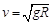
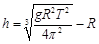
解析试题分析:设地球质量为M,若质量为m的卫星在近地轨道以第一宇宙速度v运动,则有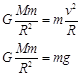
所以 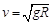
(2)设某颗地球同步卫星的质量为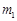 ,根据牛顿第二定律有
,根据牛顿第二定律有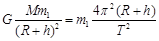
设在地球表面有一个质量为m2的物体,则有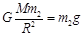
所以 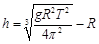
考点:本题考查万有引力在天体运动中的应用。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度约为地球公转速度的7倍,轨道半径约为地球公转道半径的2×109倍,为了粗略估算银河系中恒星的数目,可认为银河系中所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳质量,则银河系中恒星数目约为
| A.109 | B.1011 | C.1013 | D.1015 |
为了探测X星球,载着登陆舱的探测飞船在以该星球中心为圆心,半径为r1的圆轨道上运动,周期为T1,总质量为m1。随后登陆舱脱离飞船,变轨登陆X星球。则:
A.X星球的质量为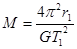 |
| B.当登陆舱脱离飞船后,飞船的运行速度不会发生变化 |
| C.研究人员在飞船内无法用弹簧测力计测量物体的重力,是因为物体不受力的作用 |
| D.登陆舱脱离飞船,变轨后想登陆X星球,登陆舱必须立即减速 |
一物体在水平面上由静止开始在水平恒力F作用下运动t s,t s末撤去该力,物体又经过2t s停止运动,在此过程中,物体受到的摩擦力大小为( )
| A.F/4 | B.F/3 | C.F/2 | D.2F/3 |
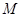 ,半径为
,半径为 ,万有引力常量为
,万有引力常量为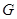 .请你结合以上数据求:
.请你结合以上数据求: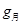 ; ②月球的第一宇宙速度
; ②月球的第一宇宙速度 ;
;