题目内容
【题目】如图所示,半径为R的半圆形区域内分布着垂直纸面向里的匀强磁场,磁感应强度为B,半圆的左边垂直x轴放置一粒子发射装置,在-R≤y≤R的区间内各处均沿x轴正方向同时发射出一个带正电粒子,粒子质量均为m、电荷量均为q、初速度均为v,重力忽略不计,所有粒子均能穿过磁场到达y轴,其中最后到达y轴的粒子比最先到达y轴的粒子晚Δt时间,则( )
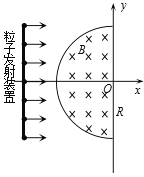
A. 粒子到达y轴的位置一定各不相同
B. 磁场区域半径R应满足![]()
C. 从x轴入射的粒子最先到达y轴
D. ![]() ,其中角度θ的弧度值满足
,其中角度θ的弧度值满足![]()
【答案】AD
【解析】粒子射入磁场后做匀速圆周运动,其运动轨迹如图所示:
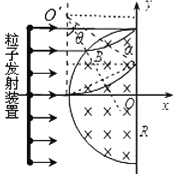
y=±R的粒子直接沿直线做匀速运动到达y轴,其它粒子在磁场中发生偏转。
A、由图可知,发生偏转的粒子也有可能打在y=R的位置上,所以粒子到达y轴的位置不是各不相同的,故A正确;B、以沿x轴射入的粒子为例,若![]() ,则粒子不能达到y轴就偏向上离开磁场区域,所以要求
,则粒子不能达到y轴就偏向上离开磁场区域,所以要求![]() ,所有粒子才能穿过磁场到达y轴,故B错误;C、从x轴入射的粒子在磁场中对应的弧长最长,所以该粒子最后到达y轴,故C错误.D、而y=±R的粒子直接沿直线做匀速运动到达y轴,时间最短;从x轴入射的粒子运动时间为:
,所有粒子才能穿过磁场到达y轴,故B错误;C、从x轴入射的粒子在磁场中对应的弧长最长,所以该粒子最后到达y轴,故C错误.D、而y=±R的粒子直接沿直线做匀速运动到达y轴,时间最短;从x轴入射的粒子运动时间为:![]() ,y=±R的粒子直接沿直线做匀速运动到达y轴,时间最短,则
,y=±R的粒子直接沿直线做匀速运动到达y轴,时间最短,则![]() ,所以
,所以![]() ,其中角度θ为从x轴入射的粒子运动的圆心角,根据几何关系有:α=θ,则
,其中角度θ为从x轴入射的粒子运动的圆心角,根据几何关系有:α=θ,则![]() ,
,![]() ,故D正确;故选AD.
,故D正确;故选AD.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目