题目内容
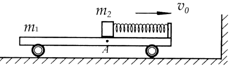 如图所示,在光滑水平地面上,有一质量m1=4.0kg的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧.位于小车上A点处质量m2=1.0kg的木块(可视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力.木块与A点左侧的车面之间的动摩擦因数μ=0.40,木块与A点右侧的车面之间的摩擦可忽略不计.现小车与木块一起以v0=2.0m/s的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以v1=1.0m/s的速度反向弹回,已知重力加速度g取10m/s2,弹簧始终处于弹性限度内.求:
如图所示,在光滑水平地面上,有一质量m1=4.0kg的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧.位于小车上A点处质量m2=1.0kg的木块(可视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力.木块与A点左侧的车面之间的动摩擦因数μ=0.40,木块与A点右侧的车面之间的摩擦可忽略不计.现小车与木块一起以v0=2.0m/s的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以v1=1.0m/s的速度反向弹回,已知重力加速度g取10m/s2,弹簧始终处于弹性限度内.求:(1)小车撞墙后弹簧的最大弹性势能;
(2)要使木块最终不从小车上滑落,则车面A点左侧粗糙部分的长度应满足什么条件?
分析:二者速度相等时弹簧的弹性势能最大,根据动量守恒定律求出二者的共同速度,然后由机械能守恒定律求出弹簧的弹性势能;
木块被弹簧弹出后滑到A点左侧某处与小车具有相同的速度v’时,木块将不会从小车上滑落,找出临界条件后根据动量守恒和能量守恒求解.
木块被弹簧弹出后滑到A点左侧某处与小车具有相同的速度v’时,木块将不会从小车上滑落,找出临界条件后根据动量守恒和能量守恒求解.
解答:解:(1)小车与墙壁碰撞后向左运动,木块与小车间发生相对运动将弹簧压缩至最短时,二者速度相等,此时弹簧的弹性势能最大,此过程中,二者组成的系统动量守恒,设弹簧压缩至最短时,小车和木块的速度大小为v,根据动量守恒定律有:
m1v1-m2v0=(m1+m2)v…①
解得 v=0.40m/s…②
设最大的弹性势能为EP,根据机械能守恒定律可得
EP=
m1v12+
m2v02-
(m1+m2)v2…③
由②③得EP=3.6J…④
(2)根据题意,木块被弹簧弹出后滑到A点左侧某处与小车具有相同的速度v’时,木块将不会从小车上滑落,此过程中,二者组成的系统动量守恒,
故有v’=v═0.40m/s…⑤
木块在A点右侧运动过程中,系统的机械能守恒,而在A点左侧相对滑动过程中将克
服摩擦阻力做功,设此过程中滑行的最大相对位移为L,根据功能关系有
μm2gL=
m1v12+
m2v02-
(m1+m2)v’2…⑥
解得L=0.90m…⑦
即车面A点左侧粗糙部分的长度应大于0.90m
答:(1)小车撞墙后弹簧的最大弹性势能3.6J.
(2)要使木块最终不从小车上滑落,则车面A点左侧粗糙部分的长度应大于0.90m.
m1v1-m2v0=(m1+m2)v…①
解得 v=0.40m/s…②
设最大的弹性势能为EP,根据机械能守恒定律可得
EP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由②③得EP=3.6J…④
(2)根据题意,木块被弹簧弹出后滑到A点左侧某处与小车具有相同的速度v’时,木块将不会从小车上滑落,此过程中,二者组成的系统动量守恒,
故有v’=v═0.40m/s…⑤
木块在A点右侧运动过程中,系统的机械能守恒,而在A点左侧相对滑动过程中将克
服摩擦阻力做功,设此过程中滑行的最大相对位移为L,根据功能关系有
μm2gL=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得L=0.90m…⑦
即车面A点左侧粗糙部分的长度应大于0.90m
答:(1)小车撞墙后弹簧的最大弹性势能3.6J.
(2)要使木块最终不从小车上滑落,则车面A点左侧粗糙部分的长度应大于0.90m.
点评:本题考查了动量守恒和能量守恒的综合运用,关键是找出木块不会从小车上滑落的临界条件,属于较难题目.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 (2008?黄冈模拟)如图所示,在光滑水平面上直线MN右侧有垂直于水平面的匀强磁场,一个电阻为R的矩形线框abcd受到水平向左的恒定拉力作用,以一定的初速度向右进入磁场,经过一段时间后又向左离开磁场.在整个运动过程中ab边始终平行于MN.则线框向右运动进入磁场和向左运动离开磁场这两个过程中( )
(2008?黄冈模拟)如图所示,在光滑水平面上直线MN右侧有垂直于水平面的匀强磁场,一个电阻为R的矩形线框abcd受到水平向左的恒定拉力作用,以一定的初速度向右进入磁场,经过一段时间后又向左离开磁场.在整个运动过程中ab边始终平行于MN.则线框向右运动进入磁场和向左运动离开磁场这两个过程中( ) 如图所示,在光滑水平面上有木块A和B,mA=0.5kg,mB=0.4kg,它们的上表面是粗糙的,今有一小铁块C,mC=0.1kg,以初速v0=20m/s沿两木块表面滑过,最后停留在B上,此时B、C以共同速度v=3m/s运动,求:
如图所示,在光滑水平面上有木块A和B,mA=0.5kg,mB=0.4kg,它们的上表面是粗糙的,今有一小铁块C,mC=0.1kg,以初速v0=20m/s沿两木块表面滑过,最后停留在B上,此时B、C以共同速度v=3m/s运动,求: 如图所示,在光滑水平面上放着长为L,质量为M的长木板,在长木板左端放一质量为m的物块(可视为质点),开始时物体和长木板均处于静止状态,物块和长木板间是粗糙的.今对物块m施一水平向右的恒力F.下列判断正确的是( )
如图所示,在光滑水平面上放着长为L,质量为M的长木板,在长木板左端放一质量为m的物块(可视为质点),开始时物体和长木板均处于静止状态,物块和长木板间是粗糙的.今对物块m施一水平向右的恒力F.下列判断正确的是( ) 如图所示,在光滑水平面上放有质量为2kg的长木板B,模板B右端距竖直墙s=4m,木板B上有一质量为1kg的金属块A,金属块A和木版B间滑动摩擦因数μ=0.20.开始A以υo=3m/s的初速度向右运动,木板B很长,A不会从B上滑下,木板B与竖直墙碰撞后以碰前速率返回,且碰撞时间极短.g取10m/s2.求
如图所示,在光滑水平面上放有质量为2kg的长木板B,模板B右端距竖直墙s=4m,木板B上有一质量为1kg的金属块A,金属块A和木版B间滑动摩擦因数μ=0.20.开始A以υo=3m/s的初速度向右运动,木板B很长,A不会从B上滑下,木板B与竖直墙碰撞后以碰前速率返回,且碰撞时间极短.g取10m/s2.求 如图所示,在光滑水平面上静止着一块质量为M=5kg的长方体木板A,木板的左端静止放置着一质量为m=2kg的物块B,已知AB之间动摩擦因数μ=0.5,经过实验发现当对物块B施加一个大小为16N水平向右的拉力F后经过2s物块B被拉到木板的右端,g取10m/s2,求:
如图所示,在光滑水平面上静止着一块质量为M=5kg的长方体木板A,木板的左端静止放置着一质量为m=2kg的物块B,已知AB之间动摩擦因数μ=0.5,经过实验发现当对物块B施加一个大小为16N水平向右的拉力F后经过2s物块B被拉到木板的右端,g取10m/s2,求: