题目内容
2. 如图,A容器容积为10L,里面充满12atm、温度为300K的理想气体,B容器是真空,现将A中气体温度升高到400K,然后打开阀门S,将A中的气体释放一部分到B容器,当A容器内压强降到4atm时,关闭阀门,这时B容器内的压强是3atm.不考虑气体膨胀过程中温度的变化,求B容器的容积.
如图,A容器容积为10L,里面充满12atm、温度为300K的理想气体,B容器是真空,现将A中气体温度升高到400K,然后打开阀门S,将A中的气体释放一部分到B容器,当A容器内压强降到4atm时,关闭阀门,这时B容器内的压强是3atm.不考虑气体膨胀过程中温度的变化,求B容器的容积.
分析 以A、B中气体为研究对象,分别研究其初、末状态,根据气体方程列式可求解
解答 解:设A容器容积为VA,温度T0=(273+27)K=300 K时,压强为p0;温度升高到T1=400 K时,压强为p1
根据查理定律有:$\frac{{P}_{0}}{{T}_{0}}$=$\frac{{P}_{1}}{{T}_{1}}$
解得:p1=16 atm
对于气体膨胀过程,为等温变化,以膨胀后A中气体为研究对象,
初态:p1′=16 atm,体积为V1′
末态:p2′=4 atm,V2′=VA=10 L
根据玻意耳定律有p1′V1′=p2′V2′
得V1′=2.5 L.
对B中气体
初态:p=16 atm V=VA-V1′=7.5 L
末态:p′=3 atm,V′=VB
同理有:pV=p′V′
得:VB=V′=40L
答:B容器的容积为 40L.
点评 本题关键找出已知状态参量,选取不同的气体作为研究对象,然后根据理想气体状态方程列方程求解

练习册系列答案
相关题目
12. 如图所示,足够长传送带与水平面的夹角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连.开始时,a、b及传送带均静止且mb>masinθ.现使传送带顺时针匀速转动,则物块在运动(物块未与滑轮相碰)过程中( )
如图所示,足够长传送带与水平面的夹角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连.开始时,a、b及传送带均静止且mb>masinθ.现使传送带顺时针匀速转动,则物块在运动(物块未与滑轮相碰)过程中( )
 如图所示,足够长传送带与水平面的夹角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连.开始时,a、b及传送带均静止且mb>masinθ.现使传送带顺时针匀速转动,则物块在运动(物块未与滑轮相碰)过程中( )
如图所示,足够长传送带与水平面的夹角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连.开始时,a、b及传送带均静止且mb>masinθ.现使传送带顺时针匀速转动,则物块在运动(物块未与滑轮相碰)过程中( )| A. | 一段时间后,a可能匀速运动 | |
| B. | 一段时间后,摩擦力对a可能做负功 | |
| C. | 开始的一段时间内,重力对a做功的功率大于重力对b做功的功率 | |
| D. | 摩擦力对a做的功等于a、b机械能的增量 |
17. 如图,空间中在边界MN的右侧存在垂直于纸面向里的匀强磁场,S是磁场中的一粒子源.某一时刻,从s平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间有多数粒子从边界MN射出磁场.已知从边界MN射出的粒子在磁场中运动的最短时间为$\frac{T}{6}$(T为粒子在磁场中运动的周期),则从边界MN射出的粒子在磁场中运动的最长时间为( )
如图,空间中在边界MN的右侧存在垂直于纸面向里的匀强磁场,S是磁场中的一粒子源.某一时刻,从s平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间有多数粒子从边界MN射出磁场.已知从边界MN射出的粒子在磁场中运动的最短时间为$\frac{T}{6}$(T为粒子在磁场中运动的周期),则从边界MN射出的粒子在磁场中运动的最长时间为( )
 如图,空间中在边界MN的右侧存在垂直于纸面向里的匀强磁场,S是磁场中的一粒子源.某一时刻,从s平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间有多数粒子从边界MN射出磁场.已知从边界MN射出的粒子在磁场中运动的最短时间为$\frac{T}{6}$(T为粒子在磁场中运动的周期),则从边界MN射出的粒子在磁场中运动的最长时间为( )
如图,空间中在边界MN的右侧存在垂直于纸面向里的匀强磁场,S是磁场中的一粒子源.某一时刻,从s平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间有多数粒子从边界MN射出磁场.已知从边界MN射出的粒子在磁场中运动的最短时间为$\frac{T}{6}$(T为粒子在磁场中运动的周期),则从边界MN射出的粒子在磁场中运动的最长时间为( )| A. | $\frac{T}{2}$ | B. | $\frac{2T}{3}$ | C. | $\frac{3T}{4}$ | D. | $\frac{5T}{6}$ |
11. 据报道:2008年北京奥运会,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输.如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯的折射率为n1,外层材料的折射率为n2,光在空气中的传播速度为c,若光从它的一端射入经全反射后从另一端射出所需的最长时间为t,则下列说法正确的是(图中所标的φ为全反射的临界角,其中sinφ=$\frac{{n}_{2}}{{n}_{1}}$)( )
据报道:2008年北京奥运会,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输.如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯的折射率为n1,外层材料的折射率为n2,光在空气中的传播速度为c,若光从它的一端射入经全反射后从另一端射出所需的最长时间为t,则下列说法正确的是(图中所标的φ为全反射的临界角,其中sinφ=$\frac{{n}_{2}}{{n}_{1}}$)( )
 据报道:2008年北京奥运会,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输.如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯的折射率为n1,外层材料的折射率为n2,光在空气中的传播速度为c,若光从它的一端射入经全反射后从另一端射出所需的最长时间为t,则下列说法正确的是(图中所标的φ为全反射的临界角,其中sinφ=$\frac{{n}_{2}}{{n}_{1}}$)( )
据报道:2008年北京奥运会,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输.如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯的折射率为n1,外层材料的折射率为n2,光在空气中的传播速度为c,若光从它的一端射入经全反射后从另一端射出所需的最长时间为t,则下列说法正确的是(图中所标的φ为全反射的临界角,其中sinφ=$\frac{{n}_{2}}{{n}_{1}}$)( )| A. | n1>n2,t=$\frac{{{n_1}L}}{{n_2^{\;}c}}$ | B. | n1>n2,t=$\frac{n_1^2L}{{n_2^{\;}c}}$ | ||
| C. | n1<n2,t=$\frac{{{n_1}L}}{{n_2^{\;}c}}$ | D. | n1<n2,t=$\frac{n_1^2L}{{n_2^{\;}c}}$ |
12.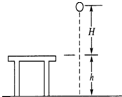 质量为m的小球,从离桌面H高处由静止下落,桌面离地高度为h,如图所示,若以桌面为参考平面,那么小球落地时的重力势能及整个过程中小球重力势能的变化分别为( )
质量为m的小球,从离桌面H高处由静止下落,桌面离地高度为h,如图所示,若以桌面为参考平面,那么小球落地时的重力势能及整个过程中小球重力势能的变化分别为( )
 质量为m的小球,从离桌面H高处由静止下落,桌面离地高度为h,如图所示,若以桌面为参考平面,那么小球落地时的重力势能及整个过程中小球重力势能的变化分别为( )
质量为m的小球,从离桌面H高处由静止下落,桌面离地高度为h,如图所示,若以桌面为参考平面,那么小球落地时的重力势能及整个过程中小球重力势能的变化分别为( )| A. | -mgh,减少mg(H+h) | B. | mgh,增加mg(H+h) | C. | -mgh,增加mg(H-h) | D. | mgh,减少mg(H-h) |
 某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并恰好越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=2.0W工作,进入竖直轨道前受到阻力f恒为0.3N,随后在运动中受到的阻力均可不计.图中L=4.00m,R=0.50m,h=1.25m,S=3.00m(取g=10m/s2)问:
某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并恰好越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=2.0W工作,进入竖直轨道前受到阻力f恒为0.3N,随后在运动中受到的阻力均可不计.图中L=4.00m,R=0.50m,h=1.25m,S=3.00m(取g=10m/s2)问: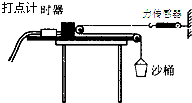 如图所示是测量物块与木板间动摩擦因数的实验装置.长木板固定在水平桌面上,打点计时器固定在长木板上,纸带穿过打点计时器,与带滑轮的物块相连.沙桶和力传感器通过绕在滑轮上的细绳相连.调整沙桶的质量,当放开沙桶时,使物块在木板上做匀加速直线运动.(重力加速度为g,滑轮的质量和摩擦可以忽略)
如图所示是测量物块与木板间动摩擦因数的实验装置.长木板固定在水平桌面上,打点计时器固定在长木板上,纸带穿过打点计时器,与带滑轮的物块相连.沙桶和力传感器通过绕在滑轮上的细绳相连.调整沙桶的质量,当放开沙桶时,使物块在木板上做匀加速直线运动.(重力加速度为g,滑轮的质量和摩擦可以忽略) 如图所示,实线OD与x轴夹角为θ=37°,在实线OD与y轴之间的范围内有电场强度方向沿y轴负方向的匀强电场,在圆O1对应的圆弧$\widehat{BD}$与线段BD所围的空间内存在方向垂直xoy平面向外的匀强磁场(未画出),一带正电的粒子从y轴上的A点以某一初速度垂直y轴射入电场,然后从B点进入磁场,到达x轴上的C点(C点存在磁场,图中没有标出)时速度方向与x轴垂直.已知$\overline{OA}$=$\overline{OB}$,粒子在磁场中的运动的周期为T、轨道半径为R,不计重力和空气阻力.
如图所示,实线OD与x轴夹角为θ=37°,在实线OD与y轴之间的范围内有电场强度方向沿y轴负方向的匀强电场,在圆O1对应的圆弧$\widehat{BD}$与线段BD所围的空间内存在方向垂直xoy平面向外的匀强磁场(未画出),一带正电的粒子从y轴上的A点以某一初速度垂直y轴射入电场,然后从B点进入磁场,到达x轴上的C点(C点存在磁场,图中没有标出)时速度方向与x轴垂直.已知$\overline{OA}$=$\overline{OB}$,粒子在磁场中的运动的周期为T、轨道半径为R,不计重力和空气阻力.