Question

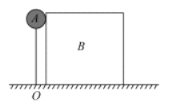
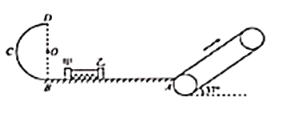
【题目】如图所示，光滑固定轨道ABCD上有两个可视为质点的滑块，滑块中间有一压缩弹簧且与两物体不拴连，左侧物体质量m1未知，右侧物体质量，轨道右侧为半径的半圆弧AB，A为圆弧最高点，B为最低点和水平面相切，左侧轨道CD为一半径为且圆心角的圆弧，转轮大小可忽略不计的粗糙的传送带EF长L=3m与水平面也成θ角，传送带沿斜面向上始终以匀速运动，传送带上表面与左端圆弧末端D点相切且刚好无弹力接触。现将两物体同时在水平轨道上由静止释放，若弹簧的弹性势能完全转化为两物体的动能，弹簧恢复原长前两物体并未进入圆弧轨道，最终m2恰好能通过右侧半圆弧A点，m1通过圆弧轨道CD滑上传送带，在传送带上一直做匀变速运动且到达F点时速度大小，m1通过传送带EF的过程中，系统摩擦生热量Q与m1的机械能变化量ΔE刚好相等，g=10m/s，sinθ=0.6，cosθ=0.8.求：

(1)m2到达B点时的速度大小vB；

(2)弹簧初始状态具有的弹性势能Ep；

(3)m1通过传送带EF的过程中，电动机额外消耗的电能上为多少。

Answer 1

【答案】(1) ；(2) ；(3) 。

【解析】

(1)由于m2刚好到达A点，则有

m2从B到A，有动能定理得

解得

(2)m1滑上传送带，最终达到F点时速度大小，且m1通过传送带EF的过程中，系统摩擦生热量Q与m1的机械能变化量刚好相等，可得

得

传送带位移

得

，

m1通过圆弧轨道CD，由动能定理得

得

两物体同时由静止释放到弹簧恢复原长过程中，系统动量守恒

得

系能机械能守恒

得

(3)物体m1通过传送带过程中，有动能定理得

物体m1对传动带的滑动摩擦力大小与电动机对传送带的牵引力大小相等，即

即

所以消耗的电能等于牵引力的功

解得