题目内容

在半径为R的某星球上，从高为h的平台上水平踢出一球，欲击中水平面上的A点，若两次踢球的方向都相同，第一次初速度为v1，着地点比A近了a，第二次初速度为v2，着地点却比A远了b，已知万有引力常量为G，求该星球的质量．
物体两次做平抛运动，两次下落高度一样，竖直方向h=
1
2
gt2，则g=
2h
t2
，①
由几何关系可知v1t+a=v2t-b，所以t=
a+b
v2-v1
，②
设星球质量为M，表面处一个物体质量为m
对表面物体，万有引力等于重力G
Mm
R2
=mg，则M=
gR2
G
 ③
联立①②③式得M=
2hR2(v2-v1)2
G(a+b)2
．
答：星球的质量M=
2hR2(v2-v1)2
G(a+b)2
．
练习册系列答案
相关题目
2005年10月12日，我国继“神舟”五号载人宇宙飞船后又成功地发射了“神舟”六号载人宇宙飞船。飞船入轨运行若干圈后成功实施变轨进入圆轨道运行，经过了近5天的运行后，飞船的返回舱于10月17日凌晨顺利降落在预定地点，两名宇航员安全返回祖国的怀抱。
设“神舟”六号载人飞船在圆轨道上绕地球运行n圈所用的时间为t，若地球表面的重力加速度为g，地球半径为R。求
(1)飞船的圆轨道离地面的高度。
(2)飞船在圆轨道上运行的速率。
欧洲开发的全球卫星定位系统“伽利略计划”进入部署和使用阶段.“伽利略计划”将发射30颗卫星，全球卫星定位系统采用的是“移动卫星”，它与电视转播用的“地球同步卫星”不同.同步卫星的轨道平面与地球赤道平面重合，离地面的高度只能为一确定的值，移动卫星的轨道离地面的高度可以改变，相应转动周期也可以不同.设某移动卫星通过地球的南、北两极的圆形轨道运行，离地面的高度为h.已知地球半径为R，地球表面的重力加速度为g,则该移动卫星连续两次通过地球赤道上空的时间间隔为_____________.
“嫦娥二号”卫星成功发射，这次发射后的卫星直接进入近地点高度200公里、远地点高度约为38万公里的地月转移轨道直接奔月，当卫星到达月球附近的特定位置时，卫星就必须“急刹车”，也就是近月制动，以确保卫星既能被月球准确捕获，又不会撞上月球，并由此进入近月点100公里、周期为12小时的椭圆轨道a，再经过两次轨道调整，进入100公里的近月圆轨道b，轨道a和b相切与P点，如图所示，下列说法正确的是（　　）
A．“嫦娥二号”卫星的发射速度大于7.9km/s，小于11.2km/s
B．“嫦娥二号”卫星的发射速度大于11.2km/s
C．“嫦娥二号”卫星在轨道a、b上经过P点时的速度大小相等
D．“嫦娥二号”卫星轨道a、b上经过P点时加速度相等
宇宙中存在一些离其它恒星很远的四颗恒星组成的四星系统，通常可忽略其它星体对它们的引力作用．稳定的四星系统存在多种形式，其中一种是四颗质量相等的恒星位于正方形的四个顶点上，沿着外接于正方形的圆形轨道做匀速圆周运动；另一种如图所示，四颗恒星始终位于同一直线上，均围绕中点O做匀速圆周运动．已知万有引力常量为G，求：
（1）已知第一种形式中的每颗恒星质量均为m，正方形边长为L，求其中一颗恒星受到的合力．
（2）已知第二种形式中的两外侧恒星质量均为m、两内侧恒星质量均为M，四颗恒星始终位于同一直线，且相邻恒星之间距离相等．求内侧恒星质量M与外侧恒星质量m的比值
M
m
．
下面所叙述的力，属于万有引力的是（　　）
A．马拉车的力
B．月球对登月舱的吸引力
C．重物所受的重力
D．地磁场对指南针的吸引力
在火箭发射阶段，宇航员发现当飞船随火箭以
g
2
的加速度匀加速上升到某位置时（g为地球表面处的重力加速度），其身下体重测试仪的示数为起动前的
17
18
，已知地球半径为R，求：
（1）该处的重力加速度g'与地表处重力加速度g的比值；
（2）火箭此时离地面的高度h．
“神舟”七号飞船的成功发射为我国在2010年实现探月计划--“嫦娥工程”获得了宝贵的经验．假设月球半径为R，月球表面的重力加速度为g0，飞船在距月球表面高度为3R的圆形轨道运行．万有引力常量为G，求：
（1）月球的质量M；
（2）月球的第一宇宙速度v；
（3）飞船在圆形轨道绕月球运行一周所需的时间T．
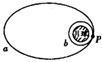
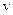若有一艘宇宙飞船在某行星表面做匀速圆周运动，若已知该行星的半径为R,其第一宇宙速度为，万有引力常量为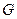，那么该行星表面的重力加速度g="             " ，该行星的平均密度为="      "         。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网