题目内容
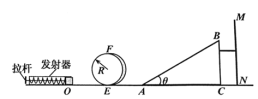
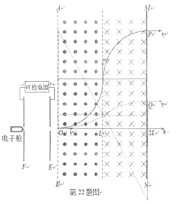
【题目】如图所示，一电子枪可以连续发射质量为m，带电量为-e的电子，两平行极板E、F分别与可控电源正、负极相接，电源电压U可在0~U0之间任意调节。电子经E、F之间的电场加速后，从x=0处沿x轴垂直磁场和边界AB进入磁场区域。已知在0≤x<L和L≤x<2L区域内分别充满垂直纸面向外和向内的匀强磁场，两磁场礅感应强度大小相等，MN是垂直x轴的足够长荧光屏。现从0开始调节电源电压至最大值U0，当电压调至
U0时，荧光屏上恰好出现亮点P (未画出)。忽略电子初速度，不计电子重力和电子间相互作用,求:
(1)磁感应强度大小；
(2)电子在磁场中运动的最短时间；
(3)设荧光屏上亮点与x轴的距离为d，请写出d与U的函数关系式。
【答案】（1）
（2）
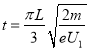（3）
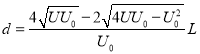
【解析】
(1) 当电压调至
时，荧光屏上恰好出现亮P，所以此时电子恰好能够进入
的磁场区域中(进入磁场时速度方向垂直x轴)，运动轨迹如图所示。设此时电子运动半径为r1，电子进入磁场时速度大小为v1，则
由几何关系:
.
联立方程，得:
(2)根据题目信息，当加速度电压为U0时，电子进入磁场时速度最大，电子在磁场中圆周运动的半径最大，电子在磁场中运动时间最短。设此时电子进入磁场时速度为v2, 电子在磁场中圆周运动半径为r2，则:
结合(1)可知，
.
根据几何关系，此时电子在两个磁场中运动转过的角度均为30°，电子在磁场中运动的总时间为
电子做圆周运动的周期
.
联立方程得
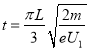
(3)设电压为U时，电子在磁场中做圆周运动的半径为r，可知:
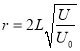
由几何关系可得:
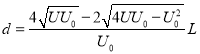
练习册系列答案
相关题目
