Question

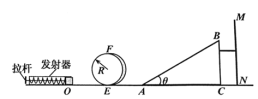
【题目】如图所示为某款弹射游戏示意图，光滑水平台面上固定发射器、竖直光滑圆轨道和粗糙斜面ABC，竖直面BC和竖直挡板MN间有一凹槽。通过轻质拉杆将发射器的弹簧压缩一定距离后释放， 滑块从O点弹出并从E点进入圆轨道，经过最高点F,离开圆轨道后继续在平直轨道上前进，从A点沿斜面AB向上运动，小球落入凹槽则游戏成功。已知滑块质量m=5g，圆轨道半径R= 5cm，斜面倾角，斜面长L= 25cm，滑块与斜面AB之间的动摩擦因数μ=0.5，忽略空气阻力，滑块可视为质点。若某次弹射中，滑块恰好运动到B点，求:

(1)滑块离开弹簧时的速度大小;

(2)滑块从B点返回到E点时对轨道的压力大小;

(3)通过计算判断滑块能否沿原轨道返回到O点?若能，则计算弹簧压缩到最短时的弹性势能;若不能，则计算出在斜面AB.上通过的总路程。(已知sin37° =0.6, cos37° =0.8)

Answer 1

【答案】（1）（2）0.15N （3）0.625m

【解析】

(1) 设滑块离开弹簧时速度大小为v0，根据动能定理:

代入数据得:

(2)设滑块从B点返回到圆轨道最低点时速度大小为v1，根据动能定理:

.

设滑块经过圆轨道最低点时受到的支持力大小为F，则:

联立方程，代入数据得:

F=3mg=0.15N

根据牛顿第三定律，滑块对轨道的压力大小为

F' =F=0.15N

(3)若滑块返回后未过圆心等高点时速度为零，其能够到达的最大高度为h，根据能量守恒

代入数据得:

h=0.05m，

正好与圆心等高，因此滑块不能沿原轨道返回到O点。

设滑块从B点下滑后在斜面上通过的路程为x，根据能量守恒:

代入数据得:

所以滑块在斜面上通过的总路程为