Question

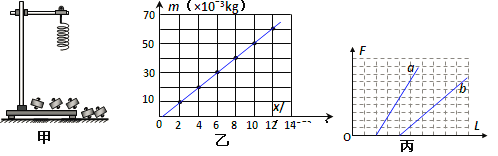
【题目】如图所示，用同种材料制成的倾斜轨道AB和水平轨道BC平滑对接于B点，整个轨道固定。现将甲、乙两物块先后从倾斜轨道的同一位置由静止释放，两物块最终停在水平轨道上的同一位置（甲乙均可视为质点）。根据上述信息，可以确定甲、乙两物块（ ）

A. 甲物体的质量要大

B. 与接触面的动摩擦因素相同

C. 损失的机械能相等

D. 乙在斜面上的平均速度要大

Answer 1

【答案】B

【解析】

对整个过程，运用动能定理列式，可得到动摩擦因数表达式，分析它们的关系，再由牛顿第二定律和运动学公式分析时间关系．根据功能关系分析机械能损失的关系。

设物块在斜面上运动的距离为s1，在水平面上运动的距离为s2，斜面的倾角为θ．动摩擦因数为μ。

对整个过程，运用动能定理得：

mgs1sinθ-μmgcosθs1-μmgs2=0-0

则得：

可知，s1、s2、θ相同，则知两个物体与轨道间的动摩擦因数相等

物体在斜面上下滑时，由牛顿第二定律得 mgsinθ-μmgcosθ=ma1，可得：a1=gsinθ-μgcosθ，所以两个物体在斜面下滑时加速度相同，

同理，在水平面上运动的加速度相同，运动时间也相同，故两个物体运动的总时间相等

由上知，不能确定两个物体质量关系，也不能判断克服摩擦力做功的大小，所以机械能损失不一定相等。

由于时间相同，位移也相同，所以平均速度相同

故应选：B。