题目内容
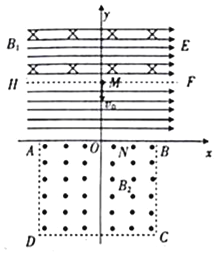
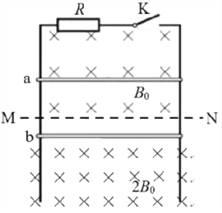
【题目】如图所示，两条足够长的平行金属导轨竖直放置，间距为
。以MN为界的两个匀强磁场，磁场方向均垂直导轨平面向里，上方区域的磁感强度大小为
，下方区域的磁感强度大小为
。金属棒a、b分处上、下磁场，质量分别为
和
，电阻均为
，与导轨接触良好，并可沿导轨无摩擦地运动。导轨上端连接一阻值为
的电阻和电键K，导轨电阻不计。重力加速度为
。
（1）若电键K断开，当a棒在竖直方向匀速运动时，b棒恰好静止，请判断a棒的运动方向，并说明理由；
（2）在第（1）问中，a棒匀速运动时所需竖直方向的外力
的大小和方向。
（3）若将a棒固定，将b棒由静止释放，运动状态稳定后再闭合电键K。请说明闭合电键后，b棒运动的速度和加速度情况，请求出b棒的最终速度。
【答案】（1）向上运动（2）
，方向竖直向上（3）
【解析】（1）当b棒静止时，受到向上的安培力作用，由左手定则可知b棒中的电流向右，a中的感应电流向左，由右手定则可知，a棒向上运动；
（2）对b棒：mg=2B0IL；
对A棒F=B0IL+2mg；
联立解得：F=
mg，方向竖直向上。
（3）开始电键K断开时，当b棒稳定后满足： 
，
解得
；当K闭合后，回路的电阻减小，电流会变大，作用在b上的安培力会变大，则b棒将做减速运动，当最后匀速运动稳定时，满足： 
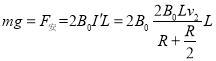，解得
练习册系列答案
相关题目
