��Ŀ����
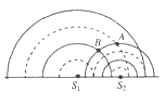
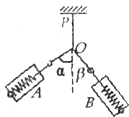
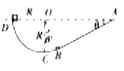
����Ŀ����ͼ��ʾ�����Ϊ��=45���Ĵֲ�ƽֱ������뾶ΪR�Ĺ⻬Բ��������У��е�ΪB���������������ֱƽ���ڣ�һ����Ϊm��С����ӹ����������Ϊh=3R��D�������»�����Բ�����������С�����Բ����ߵ�Cˮƽ�ɳ���ǡ�û��е�������Բ��O�ȸߵ�P�㣬���ƿ�����������

(1)С������C��ɳ������ʣ�
(2)��Բ����͵�ʱ�����Բ�����ѹ���Ĵ�С��
(3)������б��֮��Ķ�Ħ��������
���𰸡���1��![]() ��2��
��2��![]() ��3��0.18
��3��0.18
��������
����Ի�������˶����̷�����Ҫ���˶���Բ����͵�ʱ��Բ�����ѹ���Ĵ�С������Ҫ֪�������˶���Բ����͵�ʱ���ٶȴ�С��С�����Բ����ߵ�Cˮƽ�ɳ���ǡ�û��е�������Բ��O�ȸߵ�P�㣬����ƽ���˶����ɽ�ϼ��ι�ϵ�����͵�ʱ�ٶȣ��ڶ���͵�����ţ�ٵڶ�������⣮
��D����͵�����У��ٴ����ö��ܶ����������
�⣺��1��С�����C��ɳ�����ƽ���˶���ˮƽ�ٶ�Ϊv0��
R=gt2
R=v0t
��ã�v0=
��2��С��������͵�ʱ�ٶ�ΪV�ɻ�е���غ㶨�ɵ�
mv2=mg2R+mv02
v=
����ţ�ٵڶ����ɣ�FN��mg=m![]()
FN=6mg
����ţ�ٵ������ɵã�FN��=6mg
��3��DB֮�䳤��L=��2+1��R
��D����͵�����У��ɶ��ܶ�����
mgh����mgcos��L=mv2
��=![]() =0.18
=0.18
�𣺣�1�������˶���Բ����ߵ�Cʱ���ٶȵĴ�СΪ��
��2�������˶���Բ����͵�ʱ��Բ�����ѹ���Ĵ�СΪ6mg��
��3��������б��֮��Ķ�Ħ������Ϊ0.18��

 ��У����ϵ�д�
��У����ϵ�д�