��Ŀ����
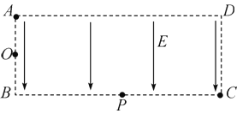
����Ŀ����ͼ��ʾ��ˮƽ��Ե�⻬���AB��B���봦����ֱƽ���ڵ�Բ���ι⻬��Ե���BCDƽ�����ӣ�Բ���İ뾶R=0.50m��������ڿռ����ˮƽ���ҵ���ǿ�糡�糡ǿ��E=1.0��104N/C������һ����m=0.06kg�Ĵ���С����Ϊ�ʵ㣩����ˮƽ�������B�˾���s=1.0m��λ�ã������ܵ��糡�������ã��������ɾ�ֹ��ʼ�˶�����֪�����������ĵ����q=8.0��10��5C��ȡg=10m/s2�����ʣ�
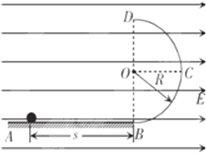
(1)����С���ܷ�Բ����ߵ�D��
(2)����С���˶����δ�ʱ�Թ����ѹ��������ֵΪ���٣�
���𰸡�(1)����С���ܵ���Բ����ߵ�D��
(2)����С���˶�������ֱ����н�Ϊ53��ʱ�Թ����ѹ��������ֵΪ5N��
��������
(1)�������С�����ع������D�㣬���ٶȴ�СΪvD���ɶ��ܶ����У�
![]()
��ʱС����D�������������Ϊ��
F��![]()
������С����Ե���Բ����ߵ�D.
(2)����С�����˶����������������糡���ĺ���Ϊ��
![]()
��������ֱ����ļн�![]()
�ʵ�С����P�㣬����POB=53��ʱ��С���Բ����ѹ�����.
��С����P����ٶȴ�СΪvP���Թ��ѹ��ΪFN���У�
![]()
![]()
��ã�FN=5N

��ϰ��ϵ�д�
 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
�����Ŀ