题目内容
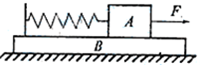如图所示，接触面光滑的A、B两物体质量分别为m和2m，由劲度系数为K的轻弹簧连接，在力F作用下，沿光滑水平面上无相对运动的向右运动，某时刻撤去外力F，则撤去F的瞬间，A、B的加速度大小分别为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：对整体分析，求出加速度，再隔离分析求出弹簧的弹力．撤去F的瞬间，弹簧的弹力不变，根据牛顿第二定律分别求出A、B的加速度．
解答：解：对整体分析，整体的加速度a=
．
隔离对B分析，F弹=2ma=
．
撤去F的瞬间，弹簧的弹力不变，
根据牛顿第二定律得，
A的加速度aA=
=
，B的加速度aB=
=
．故C正确，A、B、D错误．
故选：C．
| F |
| 3m |
隔离对B分析，F弹=2ma=
| 2F |
| 3 |
撤去F的瞬间，弹簧的弹力不变，
根据牛顿第二定律得，
A的加速度aA=
| F弹 |
| m |
| 2F |
| 3m |
| F弹 |
| 2m |
| F |
| 3m |
故选：C．
点评：解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解，注意撤去F的瞬间，弹簧的弹力不变，求出弹力是解决本题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
如图所示，接触面均光滑，球处于静止，球的重力为G=50N，请用力的分解法求：球对斜面的压力和球对竖直挡板的压力．
如图所示，在光滑的水平面上，质量分别为M、m的两木块接触面与水平支持面的夹角为θ，用大小均为F的水平力第一次向右推A，第二次向左推B，两次推动均使A、B一起在水平面上滑动，设先后两次推动中，A、B间作用力的大小分别是N1和N2，则有（ ）| A、N1：N2=m：M? | B、N1：N2=M：m?? | C、N1：N2=mcosθ：Msinθ? | D、N1：N2=Mcosθ：msinθ |
