题目内容
【题目】如图所示,在距水平地面高为h=0.5m处,水平固定一根长直光滑杆,杆上P处固定一小定滑轮,在P点的右边杆上套一质量mA=1kg的滑块A. 半径r=0.3m的光滑半圆形竖直轨道固定在地面上,其圆心O在P点的正下方,半圆形轨道上套有质量mB=2kg的小球B.滑块A和小球B用一条不可伸长的柔软细绳绕过小定滑轮相连,在滑块A上施加一水平向右的力F.若滑轮的质量和摩擦均可忽略不计,且小球可看做质点,g取10m/s2,![]() ≈0.58.
≈0.58.
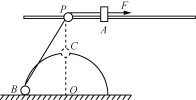
(1) 若逐渐增大拉力F,求小球B刚要离地时拉力F1的大小;
(2) 若拉力F2=57.9N,求小球B运动到C处时的速度大小;(结果保留整数)
(3) 在(2)情形中当小球B运动到C处时,拉力变为F3=16N,求小球在右侧轨道上运动的最小速度.(结果保留一位小数)
【答案】(1) 23.2N (2) 4m/s. (3) 3.2m/s.
【解析】
(1)小球刚要离地时,绳子拉力的竖直分力等于重力,列式可解;
(2)从开始到C点,对A、B整体由动能定理可解到达C点的速度;
(3)当B球的切向加速度为0时,速度最小,从C到该位置,对A、B整体由动能定理可求最小速度。
(1) F1cosα=mg,其中cosα=![]() =
=![]()
解得F1=23.2N.
(2) 当B球运动到C点时,滑块A的速度为0.对A、B整体由动能定理
F2[![]() -(h-r)]-mBgr=
-(h-r)]-mBgr=![]() mBv2
mBv2
解得v≈4m/s.
(3) 当B球的切向加速度为0时,速度取最小值vmin.此时有mgsinβ=F3
解得sinβ=0.8
对A、B整体从B球处于C位置到B球速度最小状态,用动能定理
mBgr(1-cosβ)-F3[![]() -(h-r)]
-(h-r)]
=![]() (mA+mB)v
(mA+mB)v![]() -
-![]() mBv2
mBv2
解得vmin≈3.2m/s.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目