Question

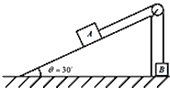
【题目】如图所示，物块A质量为2m，物块B、C质量均为m，A与天花板之间、B与C之间均用轻弹簧相连，A与B之间用细绳相连，当系统静止后，突然剪断A、B间的细绳，则此瞬间A、B、C的加速度分别为（取向下为正）

A. -g，2g，0 B. -2g，g，0

C. -4g，2g，0 D. -g，g，g

Answer 1

【答案】A

【解析】剪断细线前,对BC整体受力分析,受到总重力和细线的拉力而平衡,故 ;
剪断细线后,重力和弹簧的弹力不变,细线的拉力减为零,故物体A受到的力的合力等于,向上,根据牛顿第二定律得A的加速度为 方向向上，
物体C受到的力不变,合力为零,故C的加速度为
剪短细线后,绳子的拉力突变为零,重力和弹簧的弹力不变,故B合力大小等于绳子的拉力,方向竖直向下,
根据牛顿第二定律得B的加速度为 ，方向竖直向下，故A正确；

综上所述本题答案是：A