��Ŀ����
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxoy�ڣ��ڢ����ĵ���ֱ��������MNP�����ڴ��ڴ�ֱ������ƽ���������ǿ�ų���y��0�������ڴ�������y�����������ǿ�糡��һ����Ϊm�������Ϊq�Ĵ������Ӵӵ糡��Q����2h����h�������ٶ�v0ˮƽ���������������ԭ��O������ڢ����ޣ�����Դ�ֱ��PN�ķ�������ų�����֪MNƽ����x�ᣬN�������Ϊ��2h��2h�����������ӵ�������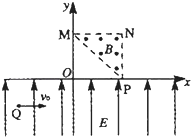
��
��1���糡ǿ�ȵĴ�СE��
��2���Ÿ�Ӧǿ�ȵĴ�СB��
��3�����Ӵ�Q���˶���N���ʱ��t��
���𰸡�
��1���⣺�����ڵ糡���˶������У���ƽ���˶����ɼ�ţ���˶����ɵã�
2h=v0t
h= ![]() at2
at2
qE=ma
������ã�
![]() ��
��
�𣺵糡ǿ�ȵĴ�СEΪ ![]() ��
��
��2���⣺���ӵ���O��ʱ����+y����ķ��ٶȣ�
![]()
�ٶ���x������ļнǦ����㣺
![]()
���Ӵ�MP���е㴹ֱ��MP����ų�����ֱ��NP����ų��������ڴų��е��ٶ� ![]() ������뾶
������뾶 ![]() ��
�� ![]() ��
��
��ã� ![]() ��
��
�𣺴Ÿ�Ӧǿ�ȵĴ�СBΪ ![]() ��
��
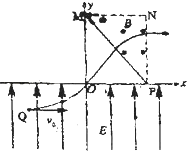
��3���⣺�����ڵ糡�е��˶�ʱ�䣺
![]()
�����ڴų��͵糡֮����˶�ʱ��Ϊ��
![]() =
= ![]()
�����ڴų��е��˶�ʱ��Ϊ��
![]()
����ʱ��Ϊ��
t= ![]() +
+ ![]() ��
��
�����Ӵ�Q���˶���N���ʱ��tΪ ![]() +
+ ![]() ��
��
����������1�����������ڵ糡������ƽ���˶���������ƽ���˶������з������E�Ĵ�С����2����������ֱ�������ȼ���ֱ���˶����ٶ�ʱ�乫ʽ���vy������tan��= ![]() ������ֵ�������ӽ���ų�ʱ���ٶȷ���������ų�ʱ���ٶȷ����ȷ��Բ����뾶��Ȼ��������������ṩ�������з������B��С����3�������ڵ糡�е��˶�ʱ�����ˮƽ���˶�ʱ�䣻�����ڴų��͵糡֮����˶�������ֱ���˶������Ӵ�Q���˶���N��������Բ���˶���Բ�Ľ�Ϊ45�㣬����t=
������ֵ�������ӽ���ų�ʱ���ٶȷ���������ų�ʱ���ٶȷ����ȷ��Բ����뾶��Ȼ��������������ṩ�������з������B��С����3�������ڵ糡�е��˶�ʱ�����ˮƽ���˶�ʱ�䣻�����ڴų��͵糡֮����˶�������ֱ���˶������Ӵ�Q���˶���N��������Բ���˶���Բ�Ľ�Ϊ45�㣬����t= ![]() ���ų��е��˶�ʱ�䣻�����͵õ���ʱ�䣮
���ų��е��˶�ʱ�䣻�����͵õ���ʱ�䣮

 ��У����ϵ�д�
��У����ϵ�д�










