��Ŀ����
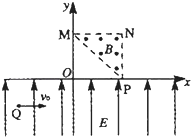
����Ŀ����ͼ����ʾ���ֲڵ�ˮƽ��������һ��ľ�����ڳ�ľ��������һ����Ϊ�ʵ�Ļ�������t=0ʱ�����������볤ľ��һ�������˶���ijʱ�̳�ľ�����Ҳ��ǽ����ײ�������̾�ֹ������������������˶������ٶȼ�Ϊ��ʱ��ǡ����ǽ�ڽӴ��������˶���v-tͼ����ͼ����ʾ���賤ľ��������Ķ�Ħ������Ϊ��1�������볤ľ��֮��Ķ�Ħ������Ϊ��2���������ٶȴ�Сȡg=10m��s2�����ʼʱ���鵽ǽ�ڵľ��뼰��Ħ��������1����2��ֵ��

���𰸡�110m��0.02��0.16
�������� (1)������Ϊ������,ľ����ǽ������ǰ,С����ľ��һ���������ȱ����˶�,���ٶ���Ϊa1��С����ľ��������ֱ�Ϊm��M����ţ�ٵڶ������У�
��1(m+M)g=(m+M)a1
��ͼ��֪,ľ����ǽ����ǰ˲ʱ�ٶ�v1=8m/s��
���˶�ѧ��ʽ�ɵã�v1=v0+a1t1
![]() ��
��
ʽ��t1=10s,x0��ľ����ǽ����ǰ�ľ���,v0��С����ľ�忪ʼ�˶�ʱ���ٶȡ�
�������ϸ�ʽ��ã���1=0.02��x0=90m.
(2)��ľ����ǽ����ײ��,С�����v1�ij��ٶ��������ȼ����˶�����С���ļ��ٶ�Ϊa2����ţ�ٵڶ������У�
��2mg=ma2
![]()
��ͼ�ɵã� ![]()
��������2=0.16��x2=20m
��ʼʱ���鵽ǽ�ڵľ���x=x1+x2=110m