题目内容
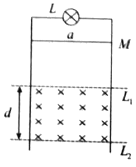
【题目】如图所示，足够长的平行光滑金属导轨竖直放置，轨道间距为L，其上端接一阻值为R的小灯泡L（阻值R保持不变）。在水平虚线L1、L2间有垂直导轨平面向里的匀强磁场，磁感应强度为B，磁场区域的宽度为d，导体棒a的质量为m、电阻为r，与导轨始终保持垂直并接触良好，设重力加速度为g。
(1)若导体棒a从图中M处由静止开始沿导轨下滑，进入磁场时恰能匀速运动，求M点距离L1的高度h；
(2)将导体棒a固定在L2处，若磁感应强度均匀增大，小灯泡始终正常发光，其额定电压为U，写出磁感应强度随时间变化的函数表达式（令t=0时，B=B0）；
(3)若导体棒a以大小为v0的初速度从L2处竖直向上运动，恰能到达L1处，求∶此过程中小灯泡产生的热量及导体棒a运动的时间。
【答案】(1)
；(2)
；(3)
【解析】
(1)导体棒
在磁场中做匀速直线运动，有
，
联立以上式子解得
(2)由题意可知
由法拉第电磁感应定律得
又有
由以上各式解得
(3)导体棒向上运动过程中，由能量守恒定律得
对小灯泡
联立解得
对导体棒由动量定理得
联立解得
练习册系列答案
名校课堂系列答案
相关题目
