题目内容
(10分)某球形天体的密度为ρ0,引力常量为G.
(1)证明对环绕密度相同的球形天体表面运行的卫星,运动周期与天体的大小无关.(球的体积公式为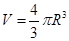 ,其中R为球半径)
,其中R为球半径)
2)若球形天体的半径为R,自转的角速度为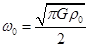 ,表面周围空间充满厚度
,表面周围空间充满厚度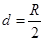 (小于同步卫星距天体表面的高度)、密度ρ=
(小于同步卫星距天体表面的高度)、密度ρ=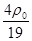 的均匀介质,试求同步卫星距天体表面的高度.
的均匀介质,试求同步卫星距天体表面的高度.
(1)证明对环绕密度相同的球形天体表面运行的卫星,运动周期与天体的大小无关.(球的体积公式为
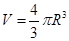 ,其中R为球半径)
,其中R为球半径)2)若球形天体的半径为R,自转的角速度为
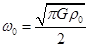 ,表面周围空间充满厚度
,表面周围空间充满厚度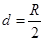 (小于同步卫星距天体表面的高度)、密度ρ=
(小于同步卫星距天体表面的高度)、密度ρ=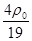 的均匀介质,试求同步卫星距天体表面的高度.
的均匀介质,试求同步卫星距天体表面的高度.(1)见解析 (2)R
试题分析:(1)设环绕其表面运行卫星的质量为m,运动周期为T,球形天体半径为R,天体质量为M,由牛顿第二定律有
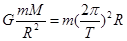 ① (2分)
① (2分)而
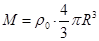 ② (1分)
② (1分)由①②式解得
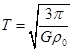 ,可见T与R无关,为一常量. (1分)
,可见T与R无关,为一常量. (1分)(2)设该天体的同步卫星距天体中心的距离为r,同步卫星的的质量为m0,则有
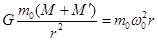 ③ (2分)
③ (2分)而
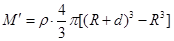 ④ (2分)
④ (2分)由②③④式解得
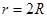 (1分)
(1分)则该天体的同步卫星距表面的高度
 (1分)
(1分)点评:中等难度。把天体运动当做匀速圆周运动,向心力来源于万有引力,再根据问题的实际情况选用恰当的公式进行计算。

练习册系列答案
相关题目
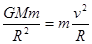 。又根据地球上的物体的重力与万有引力的关系,可以求得地球赤道表面的物体随地球自转的线速度的大小v。
。又根据地球上的物体的重力与万有引力的关系,可以求得地球赤道表面的物体随地球自转的线速度的大小v。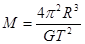
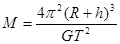
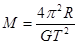

 的质点距离质量为M0的引力源中心为
的质点距离质量为M0的引力源中心为 时。其引力势能
时。其引力势能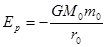 (式中G为引力常数)。现有一颗质量为
(式中G为引力常数)。现有一颗质量为 的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从
的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从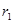 缓慢减小到
缓慢减小到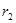 。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、
。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、