Question

【题目】如图所示，三个小球A、B、C的质量均为m，A与B、C间通过铰链用轻杆连接，杆长为L，B、C置于水平地面上，用一轻质弹簧连接，弹簧处于原长．现A由静止释放下降到最低点，两轻杆间夹角α由60°变为120°，A、B、C在同一竖直平面内运动，弹簧在弹性限度内，忽略一切摩擦，重力加速度为g．则此下降过程中（　　）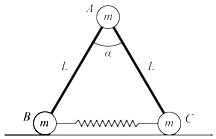

A.A的动能达到最大前，B受到地面的支持力小于 mg
B.A的动能最大时，B受到地面的支持力等于 mg
C.弹簧的弹性势能最大时，A的加速度方向竖直向下
D.弹簧的弹性势能最大值为 mgL

Answer 1

【答案】A,B
【解析】AB、A的动能最大时，设B和C受到地面的支持力大小均为F，此时整体在竖直方向受力平衡，可得2F=3mg，所以F= ；在A的动能达到最大前一直是加速下降，处于失重情况，所以B受到地面的支持力小于 mg，故A、B正确；
B、当A达到最低点时动能为零，此时弹簧的弹性势能最大，A的加速度方向向上，故C错误；
D、A下落的高度为：h=Lsin60°﹣Lsin30°，根据功能关系可知，小球A的机械能全部转化为弹簧的弹性势能，即弹簧的弹性势能最大值为EP=mgh= mgL，故D错误．
故选：AB．
A的动能最大时受力平衡，根据平衡条件求解地面支持力，根据超重失重现象分析A的动能达到最大前，B受到地面的支持力大小；根据功能关系分析弹簧的弹性势能最大值．