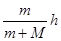题目内容
一物块沿倾角为θ的斜坡向上滑动。当物块的初速度为v时，上升的最大高度为H，如图所示；当物块的初速度为
时，上升的最大高度记为h。重力加速度大小为g。物块与斜坡间的动摩擦因数和h分别为（ ）
A．tanθ和 | B．（ －1）tanθ和 |
C．tanθ和 | D．（－1）tanθ和 |
D
解析试题分析：根据动能定理有：－mgH－μmgH/tanθ＝0－
，解得：μ＝（－1）tanθ，故选项A、C错误；当物块的初速度为时，有：－mgh－μmgh/tanθ＝0－
，解得：h＝，故选项B错误；选项D正确。
考点：本题主要考查了对动能定理（或功能关系）的理解与应用问题，属于中档题。
一个质量为0.3kg的弹性小球，在光滑水平面上以6m/s的速度垂直撞到墙上，碰撞后小球沿相反方向运动，反弹后速度大小与碰撞前相等。则碰撞前后小球速度变化量的大小△v和碰撞过程中墙对小球做功的大小W为
| A．△v =0 | B．△v = 12m/s | C．W = 0 | D．W =" 8." 10J |
ab为紧靠着的、且两边固定的两张相同薄纸，如图所示。一个质量为1kg的小球从距纸面高为60cm的地方自由下落，恰能穿破两张纸（即穿过后速度为零）。若将a纸的位置升高，b纸的位置不变，在相同条件下要使小球仍能穿破两张纸，则a纸距离b纸不超过
| A．15cm | B．20cm | C．30cm | D．60cm |
如图所示，范围足够大的匀强电场，场强大小为E，方向竖直向上．一质量为m、带电量+q的小球，在电场中以某一初速度沿电场方向做匀减速直线运动，不计空气阻力，其速度大小为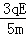
，物体运动距离为s时速度变为零，则在此过程中（ ）
A．小球克服电场力做功 qEs | B．小球的电势能增加了qEs |
| C．小球的机械能增加了qEs | D．小球的动能减少了qEs |
如图所示，在光滑绝缘水平面上有一半径为R的圆，AB是一条直径，空间有匀强电场场强大小为E，方向与水平面平行。在圆上A点有一发射器，以相同的动能平行于水平面沿不同方向发射带电量为+q的小球，小球会经过圆周上不同的点，在这些点中，经过C点的小球的动能最大。由于发射时刻不同时，小球间无相互作用，且∠α=30°。下列说法正确的是
| A．电场的方向与AC间的夹角为30° |
| B．电场的方向与AC间的夹角为60° |
C．小球在A点垂直电场方向发射，恰能落到C点，则初动能为 qER |
D．小球在A点垂直电场方向发射，恰能落到C点，则初动能为 qER |
一质量为
的物体,在水平恒定拉力的作用下以一定的初速度在粗糙的水平面上做匀速运动，当运动一段时间后,拉力逐渐减小，且当拉力减小到零时，物体刚好停止运动，图中给出了拉力随位移变化的关系图象。已知重力加速度g =10m/s2，由此可知
| A．物体与水平面间的动摩擦因数约为0.35 |
| B．减速过程中拉力对物体所做的功约为13J |
| C．匀速运动时的速度约为6m/s |
| D．减速运动的时间约为1.7s |
2010年广州亚运会上，刘翔重新回归赛场，以打破亚运记录的方式夺得110米跨栏的冠军．他采用蹲踞式起跑，在发令枪响后，左脚迅速蹬离起跑器，在向前加速的同时提升身体重心．如图所示，假设刘翔的质量为m，在起跑前进的距离s内，重心升高量为h，获得的速度为v，克服阻力做功为W阻，则在此过程中为
| A．地面的支持力对刘翔做功为mgh |
B．刘翔自身做功为 mv2＋mgh＋W阻 |
| C．刘翔的重力势能增加量为mv2＋W阻 |
| D．刘翔的动能增加量为mgh＋W阻 |