题目内容
ab为紧靠着的、且两边固定的两张相同薄纸,如图所示。一个质量为1kg的小球从距纸面高为60cm的地方自由下落,恰能穿破两张纸(即穿过后速度为零)。若将a纸的位置升高,b纸的位置不变,在相同条件下要使小球仍能穿破两张纸,则a纸距离b纸不超过
| A.15cm | B.20cm | C.30cm | D.60cm |
C
解析试题分析:若当ab为紧靠着的两边固定的两张相同的薄纸时,根据动能定理,则有:WG+Wf=0.所以Wf=-WG=-1×10×0.6J=-6J,a纸的位置升高,b纸的位置不变,在相同条件下要使小球仍能穿破两张纸,则当小球的动能达到3J时,才能穿破纸张.设释放点距a纸距离为L,根据动能定理,则有:mgL≥3J,解得:L≥30cm.因此a纸距离b纸不超过30cm.故选:C.
考点:动能定理的应用。

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案如图所示,质量为m的木箱在水平恒力F推动下,从粗糙斜面的底部A处由静止开始运动至斜面上的B处,获得速度为v,AB之间的水平距离为x、高度差为h,重力加速度为g。则在水平恒力F推动木箱从A到B的过程中,下列说法正确的是
A.木箱克服重力做的功是 |
B.合外力对木箱做的功是 |
C.推力对木箱做的功是 |
D.斜面对木箱做的功是 |
一物块沿倾角为θ的斜坡向上滑动。当物块的初速度为v时,上升的最大高度为H,如图所示;当物块的初速度为 时,上升的最大高度记为h。重力加速度大小为g。物块与斜坡间的动摩擦因数和h分别为( )
时,上升的最大高度记为h。重力加速度大小为g。物块与斜坡间的动摩擦因数和h分别为( )
A.tanθ和 | B.( -1)tanθ和 -1)tanθ和 |
C.tanθ和 | D.( -1)tanθ和 -1)tanθ和 |
如图,一质点在一恒力作用下做曲线运动,从M点运动到N点时,质点的速度方向恰好改变了90°,在此过程中,质点的动能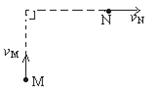
| A.不断增大 | B.不断减小 |
| C.先增大后减小 | D.先减小后增大 |
如图所示,某物体自空间O点以水平初速度v0抛出,落在地面上的A点,其轨迹为一抛物线。现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上,然后将此物体从O点由静止释放,受微小扰动而沿此滑道滑下,在下滑过程中物体未脱离滑道。P为滑道上一点,OP连线与竖直成45º角,则此物体( )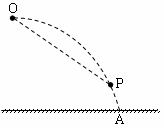
A.由O运动到P点的时间为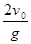 |
B.物体经过P点时,速度的水平分量为 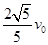 |
C.物体经过P点时,速度的竖直分量为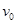 |
D.物体经过P点时的速度大小为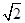 v0 v0 |
如图,固定在地面的斜面体上开有凹槽,槽内紧挨放置六个半径均为r的相同小球,各球编号如图。斜面与水平轨道OA平滑连接,OA长度为6r。现将六个小球由静止同时释放,小球离开A点后均做平抛运动,不计一切摩擦。则在各小球运动过程中,下列说法正确的是( )
| A.球1的机械能守恒 |
| B.球6在OA段机械能增大 |
| C.球6的水平射程最小 |
| D.六个球落地点各不相同 |
点电荷在匀强电场中只受电场力作用做直线运动,则该点电荷在运动过程中( )
| A.做匀变速运动 | B.电势能减少 | C.速度增加 | D.速度可能不变 |

