题目内容
甲、乙两车,从同一地点,同时开始作同向直线运动.已知甲车以速度20m/s作匀速直线运动,乙车以初速度5m/s开始作匀加速运动,加速度为1m/s2.试分析:
(1)经过多长时间,乙车落后于甲车的距离为最大?落后的最大距离是多大?此时乙车的速度多大?
(2)经过多长时间,乙车追上甲车?此时乙车的速度多大?
(1)经过多长时间,乙车落后于甲车的距离为最大?落后的最大距离是多大?此时乙车的速度多大?
(2)经过多长时间,乙车追上甲车?此时乙车的速度多大?
分析:(1)速度相等前,甲车的速度大于乙车的速度,两车的距离增大,速度相等后,甲车的速度小于乙车的速度,两车的距离减小.可知速度相等时,距离最大.根据速度相等,求出运行的时间,然后根据速度公式、位移公式求出最大距离和乙车的速度.
(2)乙车追上甲车时,两车位移相等,抓住位移相等,求出运行时间,再根据速度时间公式求出乙车的速度.
(2)乙车追上甲车时,两车位移相等,抓住位移相等,求出运行时间,再根据速度时间公式求出乙车的速度.
解答:解:(1)当两车速度相等时,两车距离最大.
经历的时间 t=
=
s=15s.
此时甲车的位移x甲=v甲t=20×15m=300m
乙车的位移x乙=v乙0t+
at2=5×15+
×1×152=187.5m.
最大距离△x=x甲-x乙=112.5m
此时乙车的速度等于甲车的速度,为20m/s.
(2)乙车追上甲车时,位移相等.
有v甲t=v乙0t+
at2,代入数据t=30s
此时乙车的速度v=v乙0+at=5+1×30m/s=35m/s.
经历的时间 t=
| v乙-v乙0 |
| a |
| 20-5 |
| 1 |
此时甲车的位移x甲=v甲t=20×15m=300m
乙车的位移x乙=v乙0t+
| 1 |
| 2 |
| 1 |
| 2 |
最大距离△x=x甲-x乙=112.5m
此时乙车的速度等于甲车的速度,为20m/s.
(2)乙车追上甲车时,位移相等.
有v甲t=v乙0t+
| 1 |
| 2 |
此时乙车的速度v=v乙0+at=5+1×30m/s=35m/s.
点评:两车从同一地点同时出发,之间的距离先增大后减小,速度相等时,距离最大.相遇时,两车的位移相等,根据位移相等,求出运行的时间,从而求出乙车的速度.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 A.选修3-3
A.选修3-3
 A.选修3-3
A.选修3-3 选做题(请从A、B和C三小题中选定两小题作答,并在答题纸上把所选题目对应字母后的方框涂满涂黑.如都作答则按A、B两小题评分)
选做题(请从A、B和C三小题中选定两小题作答,并在答题纸上把所选题目对应字母后的方框涂满涂黑.如都作答则按A、B两小题评分) D.考虑相对论效应,一条沿自身长度方向运动的杆,其长度总比杆
D.考虑相对论效应,一条沿自身长度方向运动的杆,其长度总比杆 ①波的传播方向和周期;
①波的传播方向和周期; D.德布罗意在爱因斯坦光子说的基础上提出物质波的概念,认为一切物体都具有波粒二象性。
D.德布罗意在爱因斯坦光子说的基础上提出物质波的概念,认为一切物体都具有波粒二象性。
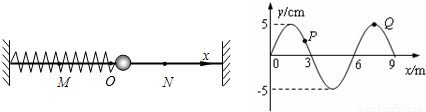
 选做题(请从A、B和C三小题中选定两小题作答,并在答题纸上把所选题目对应字母后的方框涂满涂黑.如都作答则按A、B两小题评分)
选做题(请从A、B和C三小题中选定两小题作答,并在答题纸上把所选题目对应字母后的方框涂满涂黑.如都作答则按A、B两小题评分) D.考虑相对论效应,一条沿自身长度方向运动的杆,其长度总比杆
D.考虑相对论效应,一条沿自身长度方向运动的杆,其长度总比杆 ①波的传播方向和周期;
①波的传播方向和周期; D.德布罗意在爱因斯坦光子说的基础上提出物质波的概念,认为一切物体都具有波粒二象性。
D.德布罗意在爱因斯坦光子说的基础上提出物质波的概念,认为一切物体都具有波粒二象性。