Question

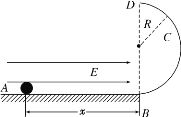
【题目】光滑绝缘的水平轨道AB与半径为R的光滑的半圆形轨道BCD相切于B点，水平轨道AB部分存在水平向右的匀强电场，半圆形轨道在竖直平面内，B为最低点，D为最高点。一质量为m、＋q的小球从距B点x的位置在电场力的作用下由静止开始沿AB向右运动，恰能通过最高点，重力加速度为g，求：

(1)电场强度的大小E；

(2)小球从开始运动到D的过程中减少的电势能；

(3)如果将同一带电小球从AB中点处由静止释放，它离开半圆轨道时离水平轨道的竖直高度。

Answer 1

【答案】(1)；(2)；(3)。

【解析】

(1)小球刚好通过圆轨道的最高点，只有重力提供向心力，

解得：

小球从A点到D点的全过程，由动能定理：

联立可得：

；

(2)小球在AB段电场力做正功，电势能减少，由功能关系得：

即电势能减少了；

(3)从AB中点处由静止释放的小球，进入圆轨道的速度偏小，将不能顺利通过最高点D，设即将离开轨道时为F点，此时的半径与竖直方向的夹角为，如图所示：

由动能定理：

在F点刚好由重力沿径向的分力提供向心力，由牛顿第二定律：

由几何关系：

联立三式解得：

。