题目内容
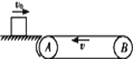
【题目】如图所示是一皮带传输装载机械示意图。井下挖掘工将矿物无初速放置于沿图示方向运行的传送带A端,被传输到末端B处,再沿一段竖直面内的圆形轨道后,从轨道的最高点C处水平抛出到货台(图中未画出)上。已知圆形轨道的半径为R=0.5m,与传送带在B点相切,O点为圆心,BO、CO分别为圆形轨道的半径,矿物视作质点,传送带与水平面间的夹角θ=37O,矿物与传送带间的动摩擦因数μ=0.8,传送带匀速运行的速度为v0=8m/s,传送带A、B点间的长度为L=45m。如果矿物被传送到B点后沿圆形轨道运动,恰好能通过最高点C,矿物质量m=50kg,sin37°=0.6,cos37°=0.8,重力加速度g取10m/s2,不计空气阻力。求:

(1)矿物被传到B点时的速度大小。
(2)矿物由B点到达C点的过程中,克服摩擦阻力所做的功。
(3)由于运送这块矿物而使电动机多输出的机械能。
【答案】(1)6m/s(2)325J(3)38400J
【解析】
先假设矿物在AB段始终加速,根据动能定理求出矿物到达B点时的速度大小,将此速度与送带匀速运行的速度v0=8m/s进行比较,确定假设是否合理;矿物被传送到B点后沿圆形轨道运动恰好能通过最高点C,说明重力提供向心力,根据牛顿第二定律求得在C点的速度;矿物由B到C过程中,重力和阻力做功,由动能定理求解克服阻力所做的功;带动传送带的电机要多输出的机械能等于滑块机械能的增加量与摩擦生热的和;
(1)假设矿物在AB段始终处于加速状态,由动能定理可得:
![]()
代入数据得![]()
由于![]() ,故假设成立,矿物到B处时的速度为6m/s
,故假设成立,矿物到B处时的速度为6m/s
(2)设矿物通过轨道最高点C处时的速度为vC,由牛顿第二定律有![]()
对矿物由B到C过程,由动能定理有![]()
解联立方程并代入数据可得矿物由B点到达C点的过程中,摩擦阻力所做的功为![]()
所以克服摩擦阻力做功为![]()
(3) 矿物在AB段运动时间为![]()
传送带与物体运动的相对位移![]()
摩擦生热![]()
带动传送带的电机要多输出的能量等于滑块机械能的增加量与摩擦生热的和,则有:
![]()

 名校课堂系列答案
名校课堂系列答案