题目内容
假如一做匀速圆周运动的人造卫星的轨道半径增大到原的2倍,仍做匀速圆周运动,则:( )
A.根据公式 ,可知卫星的线速度将增大到原的2倍
,可知卫星的线速度将增大到原的2倍
B.根据公式F= , 可知卫星所需的向心力将减小到原的
, 可知卫星所需的向心力将减小到原的
C.根据公式F=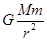 ,可知地球提供的向心力将减小到原的
,可知地球提供的向心力将减小到原的
D.根据上述B、C中给出的公式,可知卫星运动的线速度减小到原的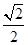
CD
解析试题分析:人造卫星做匀速圆周运动时,万有引力提供向心力,根据牛顿第二定律得: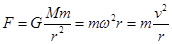 ,解得:
,解得: ,
, ,
, ,由此可以看出当轨道半径变化时,卫星的角速度、线速度、向心力随着变化,不能用
,由此可以看出当轨道半径变化时,卫星的角速度、线速度、向心力随着变化,不能用 讨论线速度的变化,故A错误; 不能用
讨论线速度的变化,故A错误; 不能用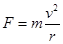 讨论向心力的变化,故B错误;
讨论向心力的变化,故B错误; 知,地球提供的向心力将减小到原的
知,地球提供的向心力将减小到原的 ,故C正确;由
,故C正确;由 知,卫星运动的线速度减小到原的
知,卫星运动的线速度减小到原的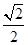 ,故D正确。所以选CD。
,故D正确。所以选CD。
考点:本题考查万有引力定律及其应用,意在考查考生角速度、线速度、加速度和半径关系的掌握情况。

两质量之比为 的卫星绕地球做匀速圆周运动,运动的轨道半径之比
的卫星绕地球做匀速圆周运动,运动的轨道半径之比 ,则下列关于两颗卫星的说法中正确的是
,则下列关于两颗卫星的说法中正确的是
A.线速度大小之比为 |
B.向心加速度大小之比为 |
C.运动的周期之比为 |
D.动能之比为 |
已知引力常数为G,月球中心到地球中心的距离为R和月球绕地球运行的周期为T。仅利用这三个数据,可以估算出的物理量有( )
| A.月球的质量 | B.地球的质量 |
| C.月球绕地球运行速度的大小 | D.地球的半径 |
已知引力常量G和下列各组数据,能计算出地球质量的是
| A.地球绕太阳运行的周期T及地球离太阳的距离r |
| B.月球绕地球运行的周期T及月球离地球的距离r |
| C.人造地球卫星在地面附近绕行的速度v及运行周期T |
| D.已知地球表面重力加速度g(不考虑地球自转) |
在牛顿发现万有引力定律一百多年之后,卡文迪许首先精确测量了引力常量。在国际单位制中引力常量的单位是
| A.N·kg2 | B.N·m2 |
| C.N·kg2/m2 | D.N·m2/kg2 |
火卫一和火卫二环绕火星做圆周运动,已知火卫一的周期比火卫二的周期小,则两颗卫星相比
| A.火卫一的线速度较大 | B.火卫一距火星表面较远 |
| C.火卫二的角速度较大 | D.火卫二的向心加速度较大 |
若已知行星绕太阳公转的半径为r,公转的周期为T,万有引力恒量为G,则由此可求出( )
| A.某行星的质量 | B.太阳的质量 |
| C.某行星的密度 | D.太阳的密度 |
“玉兔号”登月车在月球表面接触的第一步实现了中国人“奔月”的伟大梦想。机器人“玉兔号”在月球表面做了一个自由下落试验,测得物体从静止自由下落h高度的时间t,已知月球半径为R,自转周期为T,引力常量为G。则
A.月球表面重力加速度为 |
B.月球第一宇宙速度为 |
C.月球质量为 |
D.月球同步卫星离月球表面高度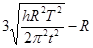 |
月球与地球质量之比约为1:80.有研究者认为月球和地球可视为一个由两质点构成的双星系统,它们都围绕月地连线上某点O做匀速圆周运动.据此观点,可知月球与地球绕O点运动的线速度大小之比约为( )
| A.1:6400 | B.1:80 | C.80:1 | D.6400:1 |