题目内容
15. 一装满苹果的箱子A放在转盘上,随着转盘以角速度ω做匀速圆周运动,在中心位置的苹果质量为m,它到转轴的距离为R(R远大于箱子),则周围苹果对该苹果的作用力为( )
一装满苹果的箱子A放在转盘上,随着转盘以角速度ω做匀速圆周运动,在中心位置的苹果质量为m,它到转轴的距离为R(R远大于箱子),则周围苹果对该苹果的作用力为( )| A. | mg | B. | mω2R | ||
| C. | $\sqrt{{m^2}{g^2}-{m^2}{ω^4}{R^2}}$ | D. | $\sqrt{{m^2}{g^2}+{m^2}{ω^4}{R^2}}$ |
分析 苹果水平方向所受合力提供向心力,由竖直方向受力平衡,根据牛顿第二定律列式求解即可.
解答 解:苹果做匀速圆周运动,合力提供向心力,受重力和弹力,根据牛顿第二定律和向心力公式,有:
水平方向:Fx=mω•2R;
竖直方向:Fy=mg;
故合力为:F=$\sqrt{{{F}_{x}}^{2}+{{F}_{y}}^{2}}=\sqrt{{m}^{2}{g}^{2}+{m}^{2}{ω}^{4}{R}^{2}}$,故D正确.
故选:D
点评 本题关键是将土豆合力分解为水平方向和竖直方向的分力,然后运用牛顿第二定律列式分析.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
5. 一列简谐横波在某时刻的波形如图所示,此时刻质点P的速度为v,经过0.2s后它的速度大小、方向第一次与v相同,再经过1.0s它的速度大小、方向第二次与v相同,则下列判断中正确的是( )
一列简谐横波在某时刻的波形如图所示,此时刻质点P的速度为v,经过0.2s后它的速度大小、方向第一次与v相同,再经过1.0s它的速度大小、方向第二次与v相同,则下列判断中正确的是( )
 一列简谐横波在某时刻的波形如图所示,此时刻质点P的速度为v,经过0.2s后它的速度大小、方向第一次与v相同,再经过1.0s它的速度大小、方向第二次与v相同,则下列判断中正确的是( )
一列简谐横波在某时刻的波形如图所示,此时刻质点P的速度为v,经过0.2s后它的速度大小、方向第一次与v相同,再经过1.0s它的速度大小、方向第二次与v相同,则下列判断中正确的是( )| A. | 波沿x轴正方向传播,且波速为10m/s | |
| B. | 波沿x轴负方向传播,且波速为20m/s | |
| C. | 质点M与质点Q的位移大小总是相等、方向总是相反 | |
| D. | 若某时刻N质点到达波谷处,则Q质点一定到达波峰处 | |
| E. | 从图示位置开始计时,在0.6s时刻,质点M偏离平衡位置的位移y=-10cm |
6.关于第一宇宙速度,下列说法中正确的是( )
| A. | 它是人造地球卫星绕地球运行的最小速度 | |
| B. | 它是人造地球卫星在近地圆轨道上的绕行速度 | |
| C. | 它是能使卫星进入近地圆轨道的最小发射速度 | |
| D. | 它是卫星在椭圆轨道上运行时近地点的速度 |
7.下列说法正确的是( )
| A. | 放射性元素的半衰期随温度升高而减小 | |
| B. | 光和运动电子都具有波粒二象性 | |
| C. | α粒子散射实验可以估算出原子核的数量级为10-10m | |
| D. | 结合能越大表示原子核中的核子结合的越紧密,原子核越稳定 |
4.一列沿x轴正方向传播的简谐机械横波,波速为2m/s.某时刻波形如图所示,下列说法正确的是( )


| A. | 这列波的周期为2s | B. | 这列波的振幅为8cm | ||
| C. | 此时x=8m处质点沿y轴负方向运动 | D. | 此时x=4m处质点的速度大小为零 |
5.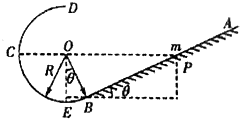 如图所示,AB是倾角θ=37°的粗糙直轨道,BCD是光滑圆弧轨道,AB恰好在B点与圆轨相切,圆轨半径R=4m.现将质量为m=5kg的小物体从直轨道上的P点由静止释放,最终它将在圆轨上往复运动.已知P点与圆轨圆心O等高,物体与轨道AB间的动摩擦因数为μ=0.2,g取10m/s2,sin37°=0.6,cos37°=0.8.则下列有关说法正确的是( )
如图所示,AB是倾角θ=37°的粗糙直轨道,BCD是光滑圆弧轨道,AB恰好在B点与圆轨相切,圆轨半径R=4m.现将质量为m=5kg的小物体从直轨道上的P点由静止释放,最终它将在圆轨上往复运动.已知P点与圆轨圆心O等高,物体与轨道AB间的动摩擦因数为μ=0.2,g取10m/s2,sin37°=0.6,cos37°=0.8.则下列有关说法正确的是( )
 如图所示,AB是倾角θ=37°的粗糙直轨道,BCD是光滑圆弧轨道,AB恰好在B点与圆轨相切,圆轨半径R=4m.现将质量为m=5kg的小物体从直轨道上的P点由静止释放,最终它将在圆轨上往复运动.已知P点与圆轨圆心O等高,物体与轨道AB间的动摩擦因数为μ=0.2,g取10m/s2,sin37°=0.6,cos37°=0.8.则下列有关说法正确的是( )
如图所示,AB是倾角θ=37°的粗糙直轨道,BCD是光滑圆弧轨道,AB恰好在B点与圆轨相切,圆轨半径R=4m.现将质量为m=5kg的小物体从直轨道上的P点由静止释放,最终它将在圆轨上往复运动.已知P点与圆轨圆心O等高,物体与轨道AB间的动摩擦因数为μ=0.2,g取10m/s2,sin37°=0.6,cos37°=0.8.则下列有关说法正确的是( )| A. | 物体从释放到最终做往复运动,在AB轨道通过的总路程为25m | |
| B. | 物体从释放到最终做往复运动,物体克服摩擦力做功为160J | |
| C. | 最终做往复运动时,物体对轨道最低点E压力大小为70N | |
| D. | 要使物体能顺利到达圆弧轨道最高点D,释放点距离E点高度差为8m |
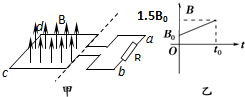 如图甲所示,在虚线左侧所示的区域有竖直向上的匀强磁场,磁场变化规律如图乙所示.边长为L的单匝正方形金属线框水平放在磁场中,线框与电阻R相连,若金属线框的电阻为0.5R.求:
如图甲所示,在虚线左侧所示的区域有竖直向上的匀强磁场,磁场变化规律如图乙所示.边长为L的单匝正方形金属线框水平放在磁场中,线框与电阻R相连,若金属线框的电阻为0.5R.求: