题目内容
3.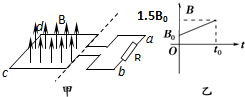 如图甲所示,在虚线左侧所示的区域有竖直向上的匀强磁场,磁场变化规律如图乙所示.边长为L的单匝正方形金属线框水平放在磁场中,线框与电阻R相连,若金属线框的电阻为0.5R.求:
如图甲所示,在虚线左侧所示的区域有竖直向上的匀强磁场,磁场变化规律如图乙所示.边长为L的单匝正方形金属线框水平放在磁场中,线框与电阻R相连,若金属线框的电阻为0.5R.求:(1)线框中产生的感应电动势的大小;
(2)流过电阻R的电流大小和方向;
(3)t0时线框cd边受到的安培力大小和方向.
分析 (1)线圈平面垂直处于匀强磁场中,当磁感应强度随着时间均匀变化时,线圈中的磁通量发生变化,从而导致出现感应电动势,产生感应电流.由法拉第电磁感应定律可求出感应电动势大小;
(2)再由闭合电路的殴姆定律可求出电流大小,再由右手定则判定感应电流方向;
(3)最后由左手定则来确定安培力的方向.
解答 解:
(1)根据法拉第电磁感应定律,则有:E=$\frac{△∅}{△t}$=$\frac{1.5{B}_{0}-{B}_{0}}{{t}_{0}}S$=$\frac{{B}_{0}{L}^{2}}{2{t}_{0}}$
(2)根据闭合电路欧姆定律,则有:I=$\frac{E}{{R}_{总}}=\frac{{B}_{0}{L}^{2}}{3R{t}_{0}}$
根据右手定则,则有:方向:a→b
(3)根据安培力表达式,则有:FA=BIL=1.5${B}_{0}×\frac{{B}_{0}{L}^{2}}{3R{t}_{0}}×L$=$\frac{{B}_{0}^{2}{L}^{3}}{2R{t}_{0}}$
根据左手定则,可知,其方向:水平向右;
答:(1)线框中产生的感应电动势的大小$\frac{{B}_{0}{L}^{2}}{2{t}_{0}}$;
(2)流过电阻R的电流大小$\frac{{B}_{0}{L}^{2}}{3R{t}_{0}}$和方向a→b;
(3)t0时线框cd边受到的安培力大小$\frac{{B}_{0}^{2}{L}^{3}}{2R{t}_{0}}$ 和方向平向右.
点评 由法拉第电磁感应定律求出感应电流的大小,而感应电流的方向则由楞次定律判定,及左手定则确定安培力的方向,同时穿过磁通量发生变化的线圈相当于电源,所以电源内部(线圈)电流方向是负极到正极,注意左手定则与右手定则的区别.

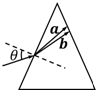 在玻璃中有一个截面为三角形的柱状真空空腔,a、b两束单色光以同样的入射角θ由玻璃射入空腔,部分光路如图,下列说法正确的是( )
在玻璃中有一个截面为三角形的柱状真空空腔,a、b两束单色光以同样的入射角θ由玻璃射入空腔,部分光路如图,下列说法正确的是( )| A. | 若增大θ,b光在空腔内先消失 | |
| B. | 若改变θ,a光通过空腔的时间一定比b光短 | |
| C. | 在同一双缝干涉装置上的干涉条纹a光较宽 | |
| D. | 若将两个相同的小球分别涂上a、b两种颜色放在同样深度的水中,在水面上看涂a颜色的小球较浅 |
| A. | 轮缘对外轨的侧压力减小 | B. | 轮缘对内轨侧压力增大 | ||
| C. | 轮缘对内、外轨无侧压力 | D. | 轮缘对外轨侧压力增大 |
| A. | 90 V | B. | 0.4 V | C. | 6 V | D. | 0 |
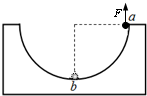 如图所示,一光滑小球在力F的作用下,以某一恒定的速率,从半径为R的固定的半圆形轨道的a点沿轨道运动到b点,作用力F的方向总是竖直向上.空气阻力不计,下面关于小球在该过程中的有关说法正确的是( )
如图所示,一光滑小球在力F的作用下,以某一恒定的速率,从半径为R的固定的半圆形轨道的a点沿轨道运动到b点,作用力F的方向总是竖直向上.空气阻力不计,下面关于小球在该过程中的有关说法正确的是( )| A. | 加速度恒定不变 | B. | 所受合外力恒定不变 | ||
| C. | 轨道的弹力不断增大 | D. | F与重力的合力恒定不变 |
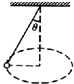 如图所示,用细线拴一小球,细线的另一端固定在天花板上,使小球在水平面内做匀速圆周运动,对于小球的运动,不变的物理量是( )
如图所示,用细线拴一小球,细线的另一端固定在天花板上,使小球在水平面内做匀速圆周运动,对于小球的运动,不变的物理量是( )| A. | 线速度 | B. | 向心力 | C. | 周期 | D. | 向心加速度 |
 一装满苹果的箱子A放在转盘上,随着转盘以角速度ω做匀速圆周运动,在中心位置的苹果质量为m,它到转轴的距离为R(R远大于箱子),则周围苹果对该苹果的作用力为( )
一装满苹果的箱子A放在转盘上,随着转盘以角速度ω做匀速圆周运动,在中心位置的苹果质量为m,它到转轴的距离为R(R远大于箱子),则周围苹果对该苹果的作用力为( )| A. | mg | B. | mω2R | ||
| C. | $\sqrt{{m^2}{g^2}-{m^2}{ω^4}{R^2}}$ | D. | $\sqrt{{m^2}{g^2}+{m^2}{ω^4}{R^2}}$ |
| A. | e′=2Emsin 2ωt | B. | e′=2Emsin 4ωt | C. | e′=4Emsin 2ωt | D. | e′=4Emsin 4ωt |