题目内容
【题目】如图所示,轮半径r很小的传送带,水平部分AB的长度L=1.5m,与一圆心在O点、半径R=1m的竖直光滑圆轨道的末端相切于A点,AB高出水平地面H=1.25m,一质量m=0.1kg的小滑块(可视为质点),由圆轨道上的P点从静止释放,OP与竖直线的夹角θ=37°.已知sin 37°=0.6,cos 37°=0.8,g=10m/s2,滑块与传送带间的动摩擦因数μ=0.1,不计空气阻力.
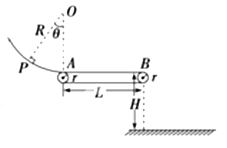
(1)求滑块对圆轨道末端的压力的大小;
(2)若传送带一直保持静止,求滑块的落地点与B间的水平距离;
(3)若传送带以v0=2.4m/s的速度沿顺时针方向运行(传送带上部分由A到B运动),求滑块从A点到B点过程中摩擦力做功的功率.
【答案】(1)1.4N;(2)0.5m;(3)0.14W
【解析】
(1)根据动能定理求得滑块到达末端A时的速度,再由牛顿第二定律求得轨道对滑块的支持力,由牛顿第三定律得滑块对圆轨道的压力;
(2)根据动能定理求得滑块离开传送带时的速度,再根据平抛知识求滑块落地点与B间的水平距离;
(3)根据牛顿第二定律求出滑块在传送带上匀加速运动时的加速度,由速度公式求出滑块加速至传送带速度时所用时间,再求摩擦力做功的功率。
(1) 滑块从P到圆轨道末端的过程中,由动能定理可得:
![]()
可得滑块到达A点时的速度:
![]()
滑块在轨道末端时,根据牛顿第二定律有:
![]()
解得:![]()
根据牛顿第三定律得:滑块对圆轨道末端的压力大小为1.4N,方向竖直向下;
(2) 从A到B的过程中,只有摩擦力对滑块做功,根据动能定理得:
![]()
代入数据可解得滑块到达B时的速度 vB=1m/s
滑块从B点开始做平抛运动,则滑块落地点距B点的水平距离:
![]() ;
;
(3) 若传送带以v0=2.4m/s的速度沿顺时针方向运行,滑块先做匀加速运动,加速度为:
![]()
从滑上传送带到与传送带共速的时间:
![]()
匀加速的位移:![]()
接着滑块做匀速运动,用时:![]()
滑块从A点到B点的总时间 t=t1+t2=0.65s
摩擦力做功为 W=μmgx1=0.1×0.1×10×0.88=0.088J
所以滑块从A点到B点过程中摩擦力做功的功率为:![]()

【题目】二极管是一种半导体元件,电路符号为![]() ,其特点是具有单向导电性。某实验小组要对一只二极管正向接入电路时的伏安特性曲线进行测绘探究。据了解,该二极管允许通过的最大电流为50mA。
,其特点是具有单向导电性。某实验小组要对一只二极管正向接入电路时的伏安特性曲线进行测绘探究。据了解,该二极管允许通过的最大电流为50mA。

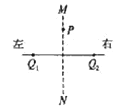
(1)该二极管外壳的标识模糊了,同学们首先用多用电表的电阻挡来判断它的正负极:当将红表笔接触二极管的左端、黑表笔接触二极管的右端时,发现指针的偏角比较小,当交换表笔再次测量时,发现指针有很大偏转,由此可判断_______ (填“左”或“右”)端为二极管的正极。
(2)实验探究中他们可选器材如下:
A.直流电源(电动势3V,内阻不计);
B.滑动变阻器(020Ω);
C.电压表(15V、内阻约80KΩ);
D.电压表(3V、内阻约50KΩ);
E.电流表(0.6A、内阻约1Ω);
F.电流表(50mA、内阻约50Ω);
G.待测二极管;
H.导线、开关。
为了提高测量精度,电压表应选用_______,电流表应选用_______。(填序号字母)
(3)实验中测量数据如下表,请在坐标纸上画出该二极管的伏安特性曲线__________。
电流I/mA | 0 | 0 | 0.2 | 1.8 | 3.9 | 8.6 | 14.0 | 21.8 | 33.5 | 50.0 |
电压U/V | 0 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | 2.25 | 2.50 |
(4)同学们将该二极管与阻值为10Ω的定值电阻串联后接到电压恒为3V的电源两端,则 二极管导通时定值电阻的功率为_______W。