题目内容
9.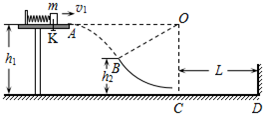 如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存了一定量的弹性势能Ep.现打开锁扣K,物块与弹簧分离后将以一定的水平速度v1向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,D处有一挡板.重力加速度g=10m/s2,空气阻力忽略不计.试求:
如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存了一定量的弹性势能Ep.现打开锁扣K,物块与弹簧分离后将以一定的水平速度v1向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,D处有一挡板.重力加速度g=10m/s2,空气阻力忽略不计.试求:(1)小物块由A到B的运动时间.
(2)压缩的弹簧在被锁扣K锁住时所储存的弹性势能Ep.
(3)若要求小物块能与挡板发生碰撞,求轨道CD与小物块间的动摩擦因数的最大值.
分析 (1)首先要清楚物块的运动过程,A到B的过程为平抛运动,已知高度运用平抛运动的规律求出时间.
(2)知道运动过程中能量的转化,弹簧的弹性势能转化给物块的动能.
(3)从A点到最后停在轨道CD上的某点p,物块的动能和重力势能转化给摩擦力做功产生的内能,根据能量守恒列出能量等式解决问题.注意根据条件分析最大动摩擦因数对应的情景.
解答 解:(1)小物块由A运动到B的过程中做平抛运动,在竖直方向上根据自由落体运动规律可知,
h=$\frac{1}{2}g{t}^{2}$
小物块由A运动到B的时间为:t=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×(1.2-0.6)}{10}}$=$\frac{\sqrt{3}}{5}$s
(2)根据图中几何关系可知,h2=h1(1-cos∠BOC)
解得:∠BOC=60°
根据平抛运动规律有:tan 60°=$\frac{gt}{v1}$
解得:v1=2 m/s
根据能的转化与守恒可知,弹簧的弹性势能为:Ep=$\frac{1}{2}$mv12=$\frac{1}{2}×1×4$=2 J
(3)依据题意知,μ的最大值对应的是物块撞墙前瞬间的速度趋于零,根据能量关系有:
mgh1+Ep≥μmgL
代入数据解得:μ≤$\frac{1}{2}$
答:(1)小物块由A到B的运动时间为$\frac{\sqrt{3}}{5}$s;
(2)压缩的弹簧在被锁扣K锁住时所储存的弹性势能Ep为2J
(3)若要求小物块能与挡板发生碰撞,轨道CD与小物块间的动摩擦因数的最大值为$\frac{1}{2}$.
点评 本题考查功能关系的应用以及平抛运动规律的应用,做物理问题应该先清楚研究对象的运动过程,根据运动性质利用物理规律解决问题.关于能量守恒的应用,要清楚物体运动过程中能量的转化.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案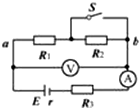 如图所示,电路中电源电动势E恒定,内阻r=2Ω,定值电阻R3=4Ω.ab段电路消耗的电功率在开关S断开与闭合时相等,电压表和电流表均为理想电表,则以下说法中正确的( )
如图所示,电路中电源电动势E恒定,内阻r=2Ω,定值电阻R3=4Ω.ab段电路消耗的电功率在开关S断开与闭合时相等,电压表和电流表均为理想电表,则以下说法中正确的( )| A. | 开关S断开时电压表的示数一定等于S闭合时的示数 | |
| B. | 电阻R1、R2可能分别为4Ω、6Ω | |
| C. | 电阻R1、R2可能分别为3Ω、9Ω | |
| D. | 开关S断开与闭合时,电压表的示数变化量与电流表的示数变化量大小之比与R1、R2无关 |
 在研究一个微型电动机的性能时,应用了图示的试验电路.闭合开关,当调节变阻器R使电动机停止转动时,电流表和电压表的示数分别为0.5A和2V;再调节R使电动机正常运转时,电流表和电压表的示数分别为2A和24V.则这个电动机正常运转时的输出功率为( )
在研究一个微型电动机的性能时,应用了图示的试验电路.闭合开关,当调节变阻器R使电动机停止转动时,电流表和电压表的示数分别为0.5A和2V;再调节R使电动机正常运转时,电流表和电压表的示数分别为2A和24V.则这个电动机正常运转时的输出功率为( )| A. | 48w | B. | 47w | C. | 32w | D. | 44w |
| A. | 研究跳水运动员的姿势时运动员可以看成质点 | |
| B. | 讨论火车从某一路标经过的时间时火车可以看成质点 | |
| C. | 讨论某同学从贵龙中学骑自行车到丁字口的时间,该自行车能看成质点 | |
| D. | ”天宫一号”与“神舟一号”对接时“神州一号”能看成质点 |
| A. | 油罐车后面装一条拖地铁链 | B. | 电工钳柄上套有一绝缘套 | ||
| C. | 飞机轮胎用导电橡胶制成 | D. | 印染车间保持适当的湿度 |
 用如图所示的方法可以研究不同人的反应时间,设直尺从静止开始自由下落到直尺被受测者抓住,直尺下落的竖直距离为h,受测者的反应时间为t,则下列关于t和h的关系正确的是( )
用如图所示的方法可以研究不同人的反应时间,设直尺从静止开始自由下落到直尺被受测者抓住,直尺下落的竖直距离为h,受测者的反应时间为t,则下列关于t和h的关系正确的是( )| A. | t∝h | B. | t∝$\frac{1}{h}$ | C. | t∝h2 | D. | t∝$\sqrt{h}$ |
| A. | 启动时乘客受到车厢作用力的方向与车运动的方向相反 | |
| B. | 进站时从关闭发动机到停下来滑行的距离与关闭发动机时的速度成正比 | |
| C. | 做匀加速运动时,第5、6节与第6、7节车厢间的作用力之比为3:2 | |
| D. | 与改为4节动车带4节拖车的动车组最大速度之比为1:2 |
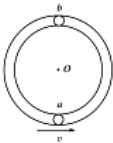 如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )| A. | 当小球b在最高点对轨道无压力时,小球a比小球b所需向心力大5 mg | |
| B. | 当v=$\sqrt{5gR}$时,小球b在轨道最高点对轨道无压力 | |
| C. | 速度v至少为$\sqrt{5gR}$,才能使两球在管内做圆周运动 | |
| D. | 只要v≥$\sqrt{5gR}$,小球a对轨道最低点的压力比小球b对轨道最高点的压力都大6 mg |
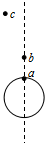
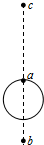
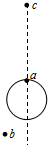
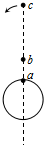 a是地球赤道上一栋建筑,b是在赤道平面内由东向西作匀速圆周运动、周期约为3.6h的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图所示),经过10天整,a、b、c的大致位置是下图中的( )
a是地球赤道上一栋建筑,b是在赤道平面内由东向西作匀速圆周运动、周期约为3.6h的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图所示),经过10天整,a、b、c的大致位置是下图中的( )