题目内容
19.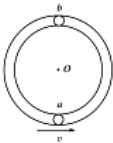 如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
如图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )| A. | 当小球b在最高点对轨道无压力时,小球a比小球b所需向心力大5 mg | |
| B. | 当v=$\sqrt{5gR}$时,小球b在轨道最高点对轨道无压力 | |
| C. | 速度v至少为$\sqrt{5gR}$,才能使两球在管内做圆周运动 | |
| D. | 只要v≥$\sqrt{5gR}$,小球a对轨道最低点的压力比小球b对轨道最高点的压力都大6 mg |
分析 要使小球能通过最高点,只要小球的速度大于零即可,而当向心力等于重力时,小球对轨道没有压力,由向心力公式可得小球在最高点时的速度,再由机械能守恒得小球在最低点的速度,以及最低点时所需要的向心力,即可求得最低点和最高点处的压力之差.
解答 解:依题意知,当小球a在最低点时,小球b在最高点,小球b在最高点对轨道无压力时,重力提供向心力即Fb=mg,由向心力公式$mg=\frac{{{mv}_{b}}^{2}}{R}$,解之得,${v}_{b}=\sqrt{gR}$,当小球a在最低点时,小球b在最高点,根据机械能守恒可知,$mg•2R+\frac{1}{2}{{mv}_{b}}^{2}=\frac{1}{2}{{mv}_{a}}^{2}$,解之得${v}_{a}=\sqrt{5gR}$.
A、根据以上计算知,当小球b在最高点对轨道无压力时,重力提供向心力,则Fb=mg,a球在最低点有${F}_{b}=\frac{{{mv}_{a}}^{2}}{R}=5mg$,所以小球a比小球b所需向心力大△F=Fa-Fb=4mg,故A错误;
B、根据以上计算当v=$\sqrt{5gR}$时,小球b在轨道最高点恰好重力提供向心力,小球b对轨道无压力,故B正确;
C、只要小球在最高点时的速度大于零,小球即可通过最高点,根据机械能守恒知,$mg•2R=\frac{1}{2}{mv}^{2}$,解之得,$v=2\sqrt{gR}$,所以速度v至少为$2\sqrt{gR}$,才能使两球在管内做圆周运动,故C错误;
D、当v≥$\sqrt{5gR}$时,管道的外壁对小球有弹力,在最高点${F}_{1}=\frac{{{mv}_{1}}^{2}}{R}-mg$,在最低点${F}_{2}=\frac{{{mv}_{2}}^{2}}{R}-mg$,由机械能守恒知$mg•2R+\frac{{{mv}_{1}}^{2}}{R}=\frac{{{mv}_{2}}^{2}}{R}$,小球a对轨道最低点的压力比小球b对轨道最高点的压力大:△F=F2-F1,以上各式联立解得,△F=6mg,即只要v≥$\sqrt{5gR}$,小球a对轨道最低点的压力比小球b对轨道最高点的压力都大6 mg.故D正确.
故选:BD.
点评 小球在竖直面内的圆周运动,若是用绳拴着只有重力小于等于向心力时,小球才能通过;而用杆或在管内运动的小球,只要在最高点时的速度大于零,小球即可通过最高点.

 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案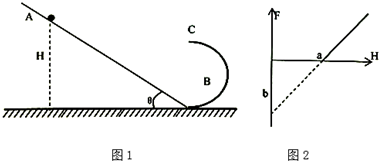
| A. | 图线的斜率与小球的质量无关 | |
| B. | b点坐标的绝对值与物块的质量成正比 | |
| C. | a的坐标与物块的质量无关 | |
| D. | 只改变斜面倾角,a、b两点的坐标均不变 |
| A. | 从能量转化的角度看,电源通过非静电力做功把其他形式的能转化为电势能 | |
| B. | 打开教室开关,日光灯立刻就亮了,表明导线中自由电荷定向运动的速率接近光速 | |
| C. | 通过导体横截面的电荷量越多,导体中的电流就越大 | |
| D. | 由公式R=U/I可知,导体的电阻与通过它的电流成反比 |
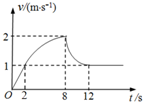 在某次消防演习中,一消防队员沿系在高处的一条悬垂的绳子由静止开始竖直滑下,经一段时间落地,运动的v-t图象如图所示,除2s~12s间的图线为曲线外,其它为直线.则下列关于消防队员的说法中正确的是( )
在某次消防演习中,一消防队员沿系在高处的一条悬垂的绳子由静止开始竖直滑下,经一段时间落地,运动的v-t图象如图所示,除2s~12s间的图线为曲线外,其它为直线.则下列关于消防队员的说法中正确的是( )| A. | 0~8s内处于超重状态,8s~12s处于失重状态 | |
| B. | 0~8s内做加速度逐渐减小的加速运动 | |
| C. | 2~8s内的平均速度等于8s~12s内的平均速度 | |
| D. | 0~8s的平均加速度不等于8s~12s的平均加速度 |
| A. | 物体加速度不为零,速度一定为零 | |
| B. | 加速度为零,物体的速度也可能变化 | |
| C. | 速度变化越快,加速度一定越大 | |
| D. | 加速度越小,速度一定越小 |
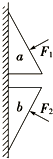 a、b为截面完全相同的直角楔形物体,分别在垂直于斜边的恒力F1、F2作用下静止在相同的竖直墙面上,如图所示,下列说法错误的是( )
a、b为截面完全相同的直角楔形物体,分别在垂直于斜边的恒力F1、F2作用下静止在相同的竖直墙面上,如图所示,下列说法错误的是( )| A. | a、b受力个数可能 不相同 | |
| B. | b受到的摩擦力一定小于a受到的摩擦力 | |
| C. | a、b所受摩擦力方向一定沿墙面向上 | |
| D. | F1、F2大小一定相等 |
| A. | 电场强度的方向就是放入电场中的电荷受到的电场力的方向 | |
| B. | 由R=$\frac{U}{I}$知道,一段导体的电阻跟它两端的电压成正比,跟通过它的电流强度成反比 | |
| C. | 场强相等的个点,电势也一定相等 | |
| D. | 导体中通过一定的电量所用的时间越短,电流强度越大 |
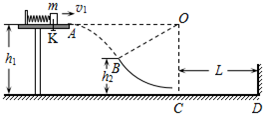 如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存了一定量的弹性势能Ep.现打开锁扣K,物块与弹簧分离后将以一定的水平速度v1向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,D处有一挡板.重力加速度g=10m/s2,空气阻力忽略不计.试求:
如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存了一定量的弹性势能Ep.现打开锁扣K,物块与弹簧分离后将以一定的水平速度v1向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,D处有一挡板.重力加速度g=10m/s2,空气阻力忽略不计.试求: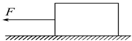 如图所示,静止在水平面上的物体,所受重力为200N,物体和水平面之间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力大小.求下列两种情况中的摩擦力:
如图所示,静止在水平面上的物体,所受重力为200N,物体和水平面之间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力大小.求下列两种情况中的摩擦力: