Question

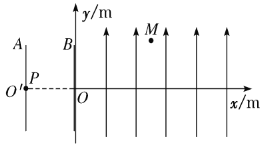
【题目】如图所示，竖直平行正对放置的带电金属板A、B，B板中心的小孔正好位于平面直角坐标系xOy的O点；y轴沿竖直方向；在x＞0的区域内存在沿y轴正方向的匀强电场，电场强度大小为V/m；比荷为C/kg的带正电的粒子P从A板中心O′处静止释放，其运动轨迹恰好经过M(4，3)点；粒子P的重力不计，试求：

(1)金属板AB之间的电势差UAB；

(2)若在粒子P经过O点的同时，在y轴右侧匀强电场中某点静止释放另一带电粒子Q，使P、Q恰能在运动中相碰；假设Q的质量是P的2倍、带电情况与P相同；粒子Q的重力及P、Q之间的相互作用力均忽略不计；求粒子Q所有释放点坐标(x，y)满足的关系。

Answer 1

【答案】(1)V (2) y＝x2，其中x＞0

【解析】

(1)设粒子P的质量为m、带电荷量为q，从O点进入匀强电场时的速度大小为v0；由题意可知，粒子P在y轴右侧匀强电场中做类平抛运动；设从O点运动到M(4，3)点历时为t0，由类平抛运动规律可得：

Eq＝ma1

xM＝v0t0

yM＝

解得：v0＝m/s

在金属板AB之间，由动能定理：

解得：UAB＝V

(2)设P、Q在右侧电场中运动的加速度分别为a1、a2；Q粒子从坐标N(x，y)点释放后，竖直向上做初速度为0的匀加速直线运动，经时间t与粒子P相遇；由牛顿运动定律及类平抛运动的规律和几何关系可得：对于P粒子：

x＝v0t

yP=

对于粒子Q：

Eq＝2ma2

yQ=

因为a2<a1，

所以粒子Q应在第一象限内释放

所以有：

yP＝y＋yQ

解得：y＝，其中x＞0

即粒子Q释放点N(x，y)坐标满足的方程为：y＝，其中x＞0。