Question

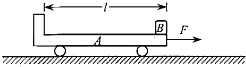
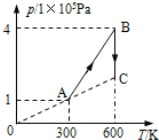
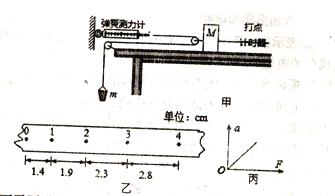
【题目】一货物传送装置如图所示，由倾角0=37。表面粗糙的固定斜槽和足够宽的水平传送带组成，斜槽与传送带垂直，末端与传送带在同一水平面上且相互靠近。传送带以恒定速度v0=3m／s向前方运动，现将一质量m=1kg可视为质点的物块，从距离斜槽底端为s=2m的顶点A处无初速度释放，物块通过斜槽底端衔接处速度大小不变，物块最终与传送带相对静止。(已知物块与斜槽间的动摩擦因数μ1=0．25，物块与传送带间的动摩擦因μ2=0．5，重力加速度为g=10m/s2，sin37°=0.6，cos37°=0.8)试求：

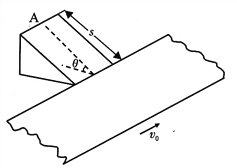
(1)物块在斜槽上的运动时间t；

(2)①物块滑上传送带时受到的摩擦力大小及方向；

②从物块滑上传送带到恰与传送带相对静止的过程中，传送带对物块的冲量大小I；

(3)物块在传送带上运动过程的最小动能EK

Answer 1

【答案】（1）1s（2）①530向左；②5Ns③2.88J

【解析】(1)物块在斜面上,受的支持力:N1=mgcosθ

摩擦力f1=μ1N1

根据牛顿第二定律：mgsinθ-f1=ma1

物块做匀加速直线运动，根据位移公式：

联立解得：

（2）①物块受传送带的摩擦力

物块滑动传送带时的速度：v2=a1t1=4 m/s

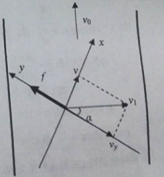
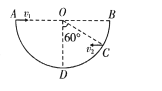
以传送带为参考系物块的速度大小为v2，方向和摩擦力方向如图所示

解得：v2=5 m/s

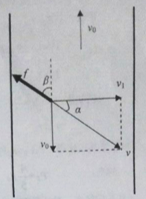
物块受摩擦力方向与v2方向相反，则α=37° β=90°-α=53°

摩擦力方向与传送带v0方向的夹角53°向左

②物块受传送带的支持力N2=mg=10N

相对传送带的加速度

相对传送带做匀减速直线运动直到停止时正好与传送带共速，根据速度公式得：t2=v2/a2=1s

物块受传送带的冲量大小：

(3)物块在传送带上运动的前阶段，合外力摩擦力方向与速度方向的夹角为钝角，摩擦力这阶段一直做负功，物块的动能一直减小，当摩擦力方向与速度方向垂直时，物块的动能最小。后阶段摩擦力方向与速度方向的夹角为锐角，摩擦力做正功，物块动能增加。建立直角坐标系如图，x方向保持匀速直线运动，y方向保持匀减速直线运动，当y方向速度减为零时，物块速度最小，即为：

最小动能