题目内容
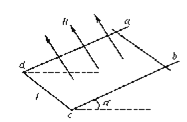
【题目】如图甲所示，一水平放置的线圈，匝数n=100匝，横截面积
，电阻
，线圈处于水平向左的均匀变化的磁场中，磁感应强度
随时间t变化关系如图乙所示。线圈与足够长的竖直光滑导轨MN、PQ连接，导轨间距L=20cm，导体棒ab与导轨始终接触良好，ab棒的电阻
，质量m=5g，导轨的电阻不计，导轨处在与导轨平面垂直向里的匀强磁场中，磁感应强度
。t=0时，导体棒由静止释放，g取
。则下列说法正确的是：（ ）
A. t=0时，线圈内产生的感应电动势大小为2V
B. t=0时，导体棒ab两端的电压为1.0V
C. t=0时，导体棒的加速度大小为
D. 导体棒ab达到稳定状态时，导体棒所受重力的瞬时功率0.25W
【答案】ACD
【解析】由图乙可知，线圈内磁感应强度变化率：
＝0.1T/s；由法拉第电磁感应定律可知：E1＝n
＝nS＝2V，选项A正确；t=0时，回路中电流为：I＝
＝0.4A，导体棒ab两端的电压为：U=IR=1.6V；设此时导体棒的加速度为a，则由：mg-B2Il=ma，得：a＝g
＝2m/s2，选项B错误，C正确；当导体棒ab达到稳定状态时，满足：mg=B2I'l，根据闭合电路的欧姆定律可得：I′＝
，代入数据解得：v=5m/s，此时导体棒所受重力的瞬时功率为：P=mgv=0.25W，选项D正确；故选ACD.
练习册系列答案
阅读快车系列答案
相关题目
