题目内容
【题目】如图所示，一光滑水平面上有质量为m的光滑曲面体A，A右端与水平面平滑连接，一质量为m的小球C放在曲面体A的斜面上，距水平面的高度为h．小球C从静止开始滑下，然后与质量为2m球B发生正碰（碰撞时间极短，且无机械能损失）．求：
（1）小球C与曲面体A分离时，A、C速度大小；
（2）小球C与小球B发生碰撞后，小球C能否追上曲面体A。
【答案】（1）
（2） 追不上
【解析】
(1) .C从曲面体滑下能量守恒，水平方向动量守恒：
设小球C与劈A分离时速度大小为v0，此时劈A速度大小为vA，小球C运动到劈A最低点的过程中，规定向右为正方向，系统水平方向动量守恒，机械能守恒，在水平方向，由动量守恒定律得：
，
由机械能守恒定律得：
解得：
A的速度向左
(2).C,B发生弹性正碰,能量守恒，动量守恒:
;
;
解得：
所以追不上
【题目】如图1所示，用“碰撞实验器”可以验证动量守恒定律，即研究两个小球在轨道水平部分碰撞前后的动量关系。O是小球抛出时球心在地面上的垂直投影点，实验时，先让入射小球m1多次从斜轨上S位置由静止释放，找到其落地点的平均位置P，测量平抛水平射程OP。然后把被碰小球m2静置于水平轨道的末端，再将入射小球m1从斜轨上S位置由静止释放，与小球m2相撞，多次重复实验，找到两小球落地的平均位置M、N。
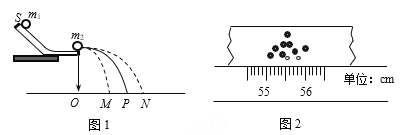
① 图2是小球m2的多次落点痕迹，由此可确定其落点的平均位置对应的读数为_______cm。
② 下列器材选取或实验操作符合实验要求的是____________。
A．可选用半径不同的两小球
B．选用两球的质量应满足m1>m2
C．小球m1每次必须从斜轨同一位置释放
D．需用秒表测定小球在空中飞行的时间
③ 在某次实验中，测量出两小球的质量分别为m1、m2，三个落点的平均位置与O点的距离分别为OM、OP、ON。在实验误差允许范围内，若满足关系式________________，即验证了碰撞前后两小球组成的系统动量守恒。（用测量的物理量表示）
④ 验证动量守恒的实验也可以在如图3所示的水平气垫导轨上完成。实验时让两滑块分别从导轨的左右两侧向中间运动，滑块运动过程所受的阻力可忽略，它们穿过光电门后发生碰撞并粘连在一起。实验测得滑块A的总质量为m1、滑块B的总质量为m2，两滑块遮光片的宽度相同，光电门记录的遮光片挡光时间如下表所示。
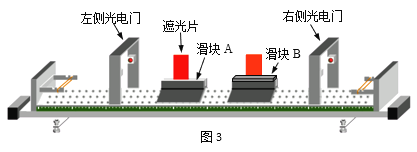
左侧光电门 | 右侧光电门 | |
碰前 | T1 | T2 |
碰后 | T3、T3 | 无 |
a．在实验误差允许范围内，若满足关系式_______________________，即验证了碰撞前后两滑块组成的系统动量守恒。（用测量的物理量表示）
b. 关于实验，也可以根据牛顿运动定律及加速的的定义，从理论上推导得出碰撞前后两滑块的动量变化量大小相等、方向相反。请写出推导过程__________（推导过程中对我用的物理量做必要的说明）。
