题目内容
10.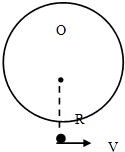 一质量m=1Kg的小球沿一光滑圆弧轨道滑下,经过圆弧最低点时速度大小为10m/s,已知圆弧轨道的半径R=5m,(g取10m/s2)求:
一质量m=1Kg的小球沿一光滑圆弧轨道滑下,经过圆弧最低点时速度大小为10m/s,已知圆弧轨道的半径R=5m,(g取10m/s2)求:(1)小球在最低点时的向心加速度;
(2)小球在最低点时对轨道的压力.
分析 (1)根据$a=\frac{{v}^{2}}{R}$求解加速度;
(2)对滑块在最低点受力分析,根据牛顿第二定律列方程即可求解.
解答 解:(1)小球在最低点时的向心加速度为:
$a=\frac{{v}^{2}}{R}=\frac{100}{5}=20m/{s}^{2}$
(2)滑块在最低点时受力分析,受重力和轨道向上的支持力,根据牛顿第二定律有:
N-mg=m$\frac{{v}^{2}}{R}$
得:N=30N
根据牛顿第三定律:N′=N=30N;
答:(1)小球在最低点时的向心加速度为20m/s2;
(2)在最低点时滑块对圆弧轨道的压力是30N
点评 解决本题的关键知道在最高点的受力情况,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
20. 惠州金山湖某小区的建设中,建筑工人用轻绳将材料运到高处,如图,使材料与竖直墙壁保持一定的距离L.在建筑材料被缓慢提起的过程中,绳AB和CD的拉力F1和F2的大小变化情况是( )
惠州金山湖某小区的建设中,建筑工人用轻绳将材料运到高处,如图,使材料与竖直墙壁保持一定的距离L.在建筑材料被缓慢提起的过程中,绳AB和CD的拉力F1和F2的大小变化情况是( )
 惠州金山湖某小区的建设中,建筑工人用轻绳将材料运到高处,如图,使材料与竖直墙壁保持一定的距离L.在建筑材料被缓慢提起的过程中,绳AB和CD的拉力F1和F2的大小变化情况是( )
惠州金山湖某小区的建设中,建筑工人用轻绳将材料运到高处,如图,使材料与竖直墙壁保持一定的距离L.在建筑材料被缓慢提起的过程中,绳AB和CD的拉力F1和F2的大小变化情况是( )| A. | F1增大,F2增大 | B. | F1增大,F2不变 | C. | F1增大,F2减小 | D. | F1减小,F2增大 |
5.关于“探究加速度与力、质量的关系”实验,下列说法中正确的是( )
| A. | 本实验采用的方法是理想化模型 | |
| B. | 探究加速度与质量的关系时,应改变拉力的大小 | |
| C. | 探究加速度与力的关系时,作a-F图象应该用线段依次将各点连接起来 | |
| D. | 探究加速度与质量的关系时,为了直观判断二者间的关系,应作出a-$\frac{1}{M}$图象 |
15.下列说法正确的是( )
| A. | 在干涉现象中振动加强的质点振幅最大,实质就是此质点发生了共振现象 | |
| B. | 我们用语言交流,是利用声波传递信息的 | |
| C. | 在惠更斯理论中,任何波的波线与波面都是相互垂直的 | |
| D. | 光纤通信具有传输容量大、衰减小、抗干扰性强等优点.是利用光的全反射原理 |
19.质量不等的两个物体,从相同高度处做自由落体运动,下列说法正确的是( )
| A. | 下落的时间不同 | B. | 落地的速度不同 | ||
| C. | 下落的加速度相同 | D. | 落地时重力势能的变化量相同 |
 甲同学采用如图所示的装置进行了“研究平抛运动”的实验.两个相同的弧形轨道M、N,分别用于发射小铁球 P、Q,其中N的末端与可看作光滑的水平板相切;两轨道上端分别装有电磁铁C、D;调节电磁铁C、D的高度,使AC=BD,从而保证小铁球P、Q在轨道出口处的水平初速度v0相等,现将小铁球P、Q分别吸在电磁铁C、D上,然后切断电源,使两小铁球能以相同的初速度v0同时分别从轨道M、N的下端射出. 随后实验可观察到PQ两球发生的现象应是P,Q二球相碰.仅仅改变弧形轨道M的高度,重复上述实验,仍能观察到相同的现象,这说明平抛运动在水平方向上是匀速运动.
甲同学采用如图所示的装置进行了“研究平抛运动”的实验.两个相同的弧形轨道M、N,分别用于发射小铁球 P、Q,其中N的末端与可看作光滑的水平板相切;两轨道上端分别装有电磁铁C、D;调节电磁铁C、D的高度,使AC=BD,从而保证小铁球P、Q在轨道出口处的水平初速度v0相等,现将小铁球P、Q分别吸在电磁铁C、D上,然后切断电源,使两小铁球能以相同的初速度v0同时分别从轨道M、N的下端射出. 随后实验可观察到PQ两球发生的现象应是P,Q二球相碰.仅仅改变弧形轨道M的高度,重复上述实验,仍能观察到相同的现象,这说明平抛运动在水平方向上是匀速运动.
 如图所示,在光滑水平面上叠放着质量为mA与mB的物体A和B(设B足够长),A与B间的动摩擦因数为μ,质量为m的小球以水平速度v射向A,以$\frac{v}{5}$的速度弹回,则A与B相对静止后的速度为$\frac{6mv}{5({m}_{A}+{m}_{B})}$.
如图所示,在光滑水平面上叠放着质量为mA与mB的物体A和B(设B足够长),A与B间的动摩擦因数为μ,质量为m的小球以水平速度v射向A,以$\frac{v}{5}$的速度弹回,则A与B相对静止后的速度为$\frac{6mv}{5({m}_{A}+{m}_{B})}$.