Question

【题目】如图所示,在xOy平面的第二象限内半径为R的圆分别与x轴、y轴相切于P、Q两点,圆内存在垂直于xOy平面向外的匀强磁场.在第一象限内存在沿y轴负方向的匀强电场,电场强度为E。一带正电的粒子(不计重力)以速率v0从P点垂直射入磁场后恰好垂直y轴进入电场,最后从M(3R,0)点射出电场,出射方向与x轴正方向夹角为α,且满足α=45°,求:

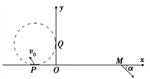
(1)带电粒子的比荷;

(2)匀强磁场的磁感应强度B的大小;

(3)粒子从P点射入磁场到从M点射出电场所经历的时间。

Answer 1

【答案】(1) ；(2) ；(3) +R；

【解析】(1)设粒子在y轴上的N点进入电场，则粒子从N到M的过程中做类平抛运动，设粒子从N到M经历的时间为t3，由类平抛规律知

vy=at3，3R=v0t3

在M点:tanα=

由牛顿第二定律知qE=ma

联立解得.

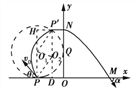
(2)粒子运动轨迹如图所示，设O1为磁场的圆心，O2为粒子做圆周运动的圆心，P'为粒子射出磁场的位置，则P'O2∥PO1，△O1O2P'与△O1O2P全等，粒子的轨道半径为r=R

粒子在磁场中由洛伦兹力提供向心力

Bqv0=m

解得B=.

(3)由(1)知粒子从N到M经历的时间为t3=，且有ON=a

代入t3得ON=R

由几何关系知ON=R+Rcosθ

则θ=

设粒子从P到P'的时间为t1，则t1=T,其中T=

解得t1=

由几何关系知P'N=R-Rsinθ

设粒子从P'到N的时间为t2，则t2=R

所以粒子从P到M所用的总时间t=t1+t2+t3=+R.