题目内容
(18分)如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧
区域Ⅰ内存在磁感应强度大小B1=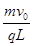 、方向垂直纸面向外的匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为(– 2L,–
、方向垂直纸面向外的匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为(– 2L,– L)的A点以速度v0沿+x方向射出,恰好经过坐标为[0,-(
L)的A点以速度v0沿+x方向射出,恰好经过坐标为[0,-( –1)L]的C点射入区域Ⅰ。粒子重力忽略不计。
–1)L]的C点射入区域Ⅰ。粒子重力忽略不计。

⑴求匀强电场的电场强度大小E;
⑵求粒子离开区域Ⅰ时的位置坐标;
⑶要使粒子从区域Ⅱ上边界离开磁场,可在区域Ⅱ内加垂直纸面向内的匀强磁场。试确定磁感应强度B的大小范围,并说明粒子离开区域Ⅱ时的速度方向。
【答案】
(1)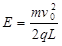 (2)(L,0)(3)
(2)(L,0)(3)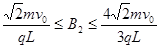 带电粒子离开磁场时速度方向与
带电粒子离开磁场时速度方向与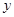 轴正方向夹角
轴正方向夹角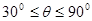
【解析】
试题分析:⑴ 带电粒子在匀强电场中做类平抛运动.
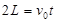 1分
1分
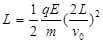 1分
1分
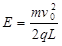 2分
2分
⑵ 设带电粒子经C点时的竖直分速度为 vy:、速度为v
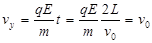 2分
2分
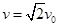 ,方向与
,方向与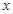 轴正向成45° 斜向上
2分
轴正向成45° 斜向上
2分
粒子进入区域Ⅰ做匀速圆周运动,
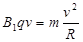
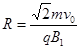
解得: 2分
2分
由几何关系知,离开区域时的位置坐标: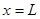
 2分
2分
⑶ 根据几何关系知,带电粒子从区域Ⅱ上边界离开磁场的半径满足
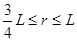 2分
2分
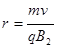
得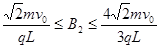 2分
2分
根据几何关系知,带电粒子离开磁场时速度方向与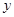 轴正方向夹角
轴正方向夹角
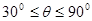 2分
2分

考点:带电粒子在匀强磁场中的运动(类平抛运动强调运动的分解,匀速圆周运动强调几何关系确定半径与已知长度的关系),牛顿第二定律,向心力

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 (2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求:
(2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求: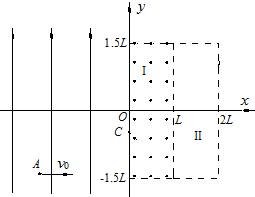 如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1=
如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1= (2006?连云港二模)如图所示,在xoy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B,方向垂直于xoy平面向里.在O点处原来静止着一个具有放射性的原子核--氮(
(2006?连云港二模)如图所示,在xoy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B,方向垂直于xoy平面向里.在O点处原来静止着一个具有放射性的原子核--氮( 如图所示,在xOy平面上,一个以原点O为圆心,半径为4R的原型磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(-2R,0)的A处静止着一个具有放射性的原子核氮713N.某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从A处射出时速度方向垂直于x轴,且后来通过了y轴,而反冲核刚好不离开磁场区域.不计重力影响和离子间的相互作用.
如图所示,在xOy平面上,一个以原点O为圆心,半径为4R的原型磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(-2R,0)的A处静止着一个具有放射性的原子核氮713N.某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从A处射出时速度方向垂直于x轴,且后来通过了y轴,而反冲核刚好不离开磁场区域.不计重力影响和离子间的相互作用.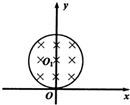 如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场.一个比荷
如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场.一个比荷