Question

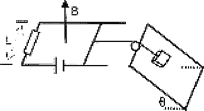
【题目】如图所示，有一固定在水平地面的光滑平台。平台右端B与静止的水平传送带平滑相接，传送带长L=4m.有一个质量为m=0.5kg的滑块，放在水平平台上，平台上有一根轻质弹簧，左端固定，右端与滑块接触但不连接，现将滑块缓慢向左移动压缩弹簧，且弹簧始终在弹性限度内，在弹簧处于压缩状态时，若将滑块由静止释放，滑块最后恰能到达传送带右端C点。已知滑块与传送带间的动摩擦因数，

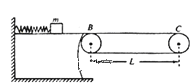
求：(1)滑块到达B点时的速度，及弹簧储存的最大弹性势能；

(2)若传送带以3.0m/s的速度沿顺时针方向匀速转动，当滑块冲上传送带时，对滑块施加一大小恒为0.5N的水平向右的作用力，滑块从B运动到C的过程中,摩擦力对它做的功；

Answer 1

【答案】(1)vB=4m/s, Ep=4J (2)Wf= -3.75J

【解析】

（1）滑块从释放至运动到B点，由能量守恒得，
Ep＝mvB2 ①
从B到C，由动能定理得，μmgL＝0mvB2 ②
联立①②两式，代入数据解得vB=4m/s
弹簧的弹性势能转化为滑块的动能：Ep＝mvB2=4J

（2）加力F后，由于vB＞v传，滑块滑上传送带时，加速度大小为a，有：μmg-F=ma1解得a1=1m/s2
滑块减速的时间

滑块减速的位移

故滑块之后匀速运动，从B到C，由动能定理得，FL+Wf＝mv传2mvB2
代入数据解得Wf=-3. 75J。