题目内容
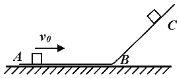
【题目】如图所示，竖直平面内的光滑四分之一圆弧轨道与水平传送带相切于 B 点，圆弧轨道的半径为 R，传送带的长为 2R，传送带上表面离地高也为 R，一质量为 m 的物块在圆弧轨道的上端 A 点正上方由静止下落，刚好能从 A 点进入圆弧轨道，若物块与传送带间的动摩擦因数
= 0.75，重力加速度为 g，空气阻力不计。
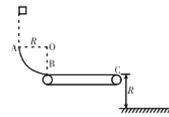
（1）若传送带静止不动，要使物块不能从传送带右端滑离，物块从 A 点正上方释放的高度应满足什么条件？
（2）若传送带逆时针运动，物块滑离传送带后落在地面上的位置离传送带右端 C 的水平距离为 2R，则物块在 B 点时对圆弧轨道的压力为多大？
（3）若某次传送带以
速度逆时针匀速运动，物块从右侧离开传送带的速度也为，求这 次物块与传送带间由于摩擦产生的热量Q.
【答案】（1）高度应小于等于0.5R（2）6mg（3）2.5mgR
【解析】
（1）对小物块，根据动能定理：
物块释放的高度应小于等于0.5R；
（2）由平抛规律可得：
由动能定理：
解之得：
根据牛顿第三定律，可得物块在B点对圆弧轨道的压力为
（3）小物块在传送带上运动时间为
，相对路程
小物块到达B点的速率为
所以
(其中
)
练习册系列答案
相关题目
